第一章
映射与函数
数列\函数 的极限
- 如果收敛则极限唯一
- 如果收敛则有界
- 如果收敛则局部保号
- 如果收敛则子列收敛
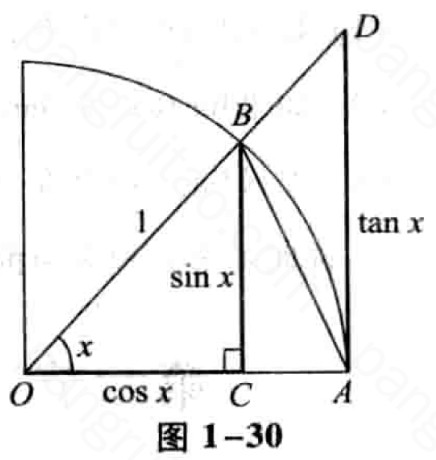
两个重要极限
\begin{align}
\lim_{x \to \inf}(1+\frac{1}{x})^x=e
\end{align}
\begin{align}
\lim_{x \to 0}\frac{\sin x}{x}=1
\end{align}
- 有界则有上确界
- 单调且有界则有极限
柯西数列收敛,收敛数列为柯西数列
函数连续性
- 连续函数复合也连续
- 连续函和、差、积、商连续
函数间断点
- 第一类间断点:左右极限都存在
- 第二类间断点:左右极限不都存在
闭区间有界函数有最大最小值
零点定理、介值定理
一致连续
第二章
导数定义
和、差、积、商、反函数、复合求导法则
高阶导数
- 莱布尼兹公式
隐函数导数
参数方程导数
微分定义
和、差、积、商、复合(形式不变性)求微分法则
第三章
微分中值定理
- 罗尔定理
- 拉格朗日中值定理
- 柯西中值定理
洛必达法则
泰勒公式
- 佩亚诺余项
- 拉格朗日余项
函数单调性和凹凸性(拐点)
函数极值(大于或小于其邻域所有,不含等号)
函数最大最小值
函数图形描绘
曲率 K
曲率半径 1/K
第四章 不定积分
原函数
换元积分
第五章 定积分
牛顿-莱布尼兹公式
偶函数奇函数周期函数积分性质
\begin{align}
\int_0^{\pi}xf(\sin x)dx = \frac{\pi}{2}\int_0^{\pi}f(\sin x)dx$
\end{align}
\begin{align}
\int_0^{\frac{\pi}{2}}\sin^n x dx = \int_0^{\frac{pi}{2}}\cos^n x dx
\end{align}
有界函数反常积分
无界函数反常积分
- 无穷限审敛
- 原函数有上届
- 比较审敛
- 和幂级数比
- 绝对收敛必定收敛
- 无界的审敛法
- 比较审敛
- 和幂级数比
- 极限审敛
- 如果存在 \(q<1\) 使 \(\lim_{x \to a^+}(x-a)^qf(x) \) 存在则收敛
- 如果 \(\lim_{x \to a^+}(x-a)f(x)>0\) 则发散
- 比较审敛
Gamma 函数
\begin{align}
\Gamma(s)=\int_0^{+\infty} e^{-x}x^{s-1} dx
\end{align}
几何学上定积分
- 极坐标
- 旋转体体积
- 曲线弧长
物理上应用
- 水压
- 引力\(F=G*m_1*m_2/r^2\)
第七章 微分方程
可分离变量的微分方程
齐次方程
一阶线形微分方程
- 齐次
- 非齐次
- 转换至线形微分方程
- 伯努利方程
- 最低阶代换
\(y^{”}=f(y,y^{‘})\) 型,令 \(p = y^{‘}\)
常系数线形微分方程
常系数非齐次线性微分方程
- 求特解
- \(f(x)=e^{\lambda x}P_m(x)\) 型
- y^{*}=x^kR_m(x)e^{\lambda x}
- \(f(x)=e^{\lambda x}(P(x)\cos wx + Q(x)\sin wx)\)
- \(f(x)=e^{\lambda x}P_m(x)\) 型
欧拉方程
第八章 向量代数与解析几何
方向角、方向余弦
数量积、向量积、混合积(张量行列式)
平面及方程
- 点法式
- 一般方程
曲面及其方程
- 旋转曲面
- 柱面
- 二次曲面
空间曲线及方程
- 一般方程
- 参数方程
- 曲线在坐标面上的投影
第九章 多元函数微分法
内点、外点、边界点、聚点、开集、闭集、连通集、区域、闭区域、有界集、无界集
极限
闭区域连续函数必有界且有最大值最小值
介值定理
一致连续性定理
偏导数、高阶偏导数
全微分:从自变量增量 到 因变量增量 的线形变换
- 充分条件 偏导连续
多元复合函数求导法则
隐函数求导公式
空间曲线的切线与法平面
曲面的切平面与法线
方向导数与梯度
- 梯度场是势场
多元函数极值
- 必要条件:偏导为0
- 充分条件\(f_{xx}*f_{yy}-f_{xy}*f_{yx} > 0\)
- \(f_{xx}*f_{yy}-f_{xy}*f_{yx} < 0\) 无极值
- \(f_{xx}*f_{yy}-f_{xy}*f_{yx} = 0\) 不确定
条件极值
- 拉格朗日乘数法
二元泰勒公式
第十章 重积分
笛卡尔坐标下二重积分
极坐标下二重积分
直角坐标三重积分
柱面坐标三重积分
球面坐标三重积分
应用
- 曲面面积
- 质心
- 转动惯量
- 引力
含参变量重积分(莱布尼兹公式)
\begin{align}
g^{‘}(x) & = \frac{d}{dx}\int_{a(x)}^{b(x)}f(x,t)dt \\
& = \int_{a(x)}^{b(x)}f_x(x,t)dt + f(x,a(x))*a^{‘}(x) – f(x,b(x))*b^{‘}(x)
\end{align}
第十一章 曲线积分与曲面积分
对弧长的曲线积分
对坐标的曲线积分
格林公式
曲线积分与路径无关的条件(势场)
全微分求积(固定起点曲线积分)
对面积的曲面积分
对坐标的曲面积分
高斯公式
任意闭曲面积分为零(无源场)
通量、散度
斯托克斯公式(空间中的格林公式)
环流量、散度
第十二章 无穷级数
柯西审敛原理
正项级数审敛法
- 充分必要:部分和有界
- 比较审敛法
- 普通形式
- 极限形式
- 比值审敛法(d’Alembert 判别法):\(\lim_{n \to +\infty}u_{n+1}/u_{n} = p\) ,p>1发散,p<1收敛,p=1不确定
- 可惜判别法:\(\lim_{n \to \infty} \sqrt[n]{u_n}=p\),p>1发散,p<1收敛,p=1不确定
交错级数审敛法
- 莱布尼兹定理
- 绝对收敛/条件收敛
幂级数
- 收敛半径 \(1 /( \lim_{n \to \infty}|a_{n+1}/a_{n}|)\)
- 幂级数的加减乘保持较小方的收敛半径,出发缩减收敛半径。积分和求导不改变收敛半径
傅立叶级数
正弦级数、余弦级数
周期为 2p 的周期函数的傅立叶级数
\begin{align}
f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty}(a_k \cos \frac{n\pi x}{p} + b_k \sin \frac{n\pi x}{p})
\end{align}
其中
\begin{align}
a_n & = \frac{1}{p} \int_{-p}^{p}f(x) \cos \frac{n \pi x}{p} dx \\
b_n & = \frac{1}{p} \int_{-p}^{p}f(x) \sin \frac{n \pi x}{p} dx
\end{align}