GAME101笔记汇总
13.Ray Tracing 1
13.1 Ray Tracing Introduction

使用光线追踪目的自然是为了解决光栅化做得还不够好的一些问题。
由于光栅化的算法原理,有很多表现上的限制,比如:
- 无法表现真实的软阴影
- 无法表现毛玻璃等粗糙的反射效果
- 无法表现非直接光照(只能用全局光照代替)

所以对比起来,光栅化快,但是效果差。

而光线追踪速度慢,但是效果好
13.2 Basic Ray Tracing Algorithm

对光线有一些基本性质的假设(和真实光仍略有区别)。

曾经很多人以为眼睛能看到东西,是类似于蝙蝠一般,由眼睛发射出“感知光线”,并且此理论被很多名人或哲学家支持。
现在来看,这种理论虽然有问题,但基于图形学中的“光路可逆性”而言,为了效率,渲染时采取的方法正是从摄像机发出“感知光线”进行渲染。
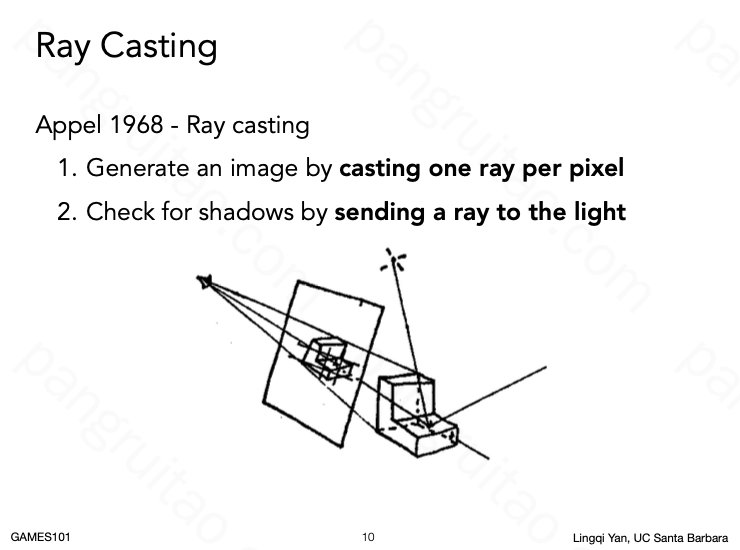
Ray Casting 方式就是从摄像机,沿每个像素发射出感知光线,并考虑其是否能被光源照亮,可以的话则计算着色。

对于一个场景而言,则需要找“感知光线”达到的第一个面
13.3 Whitted-Style Ray Tracing

将光线进行多次的弹射或折射。即是 Whitted 光线追踪。

每次弹射或者折射出新光线后,当新光线碰撞到某个面之后,再基于光源进行着色,并考虑损耗,最后加和到最初的像素点。
总之就是在模拟光线传播的过程。
但这个过程理解容易,但在实现时会有不少技术问题,下面依次结果
13.4 Ray-Surface Intersection
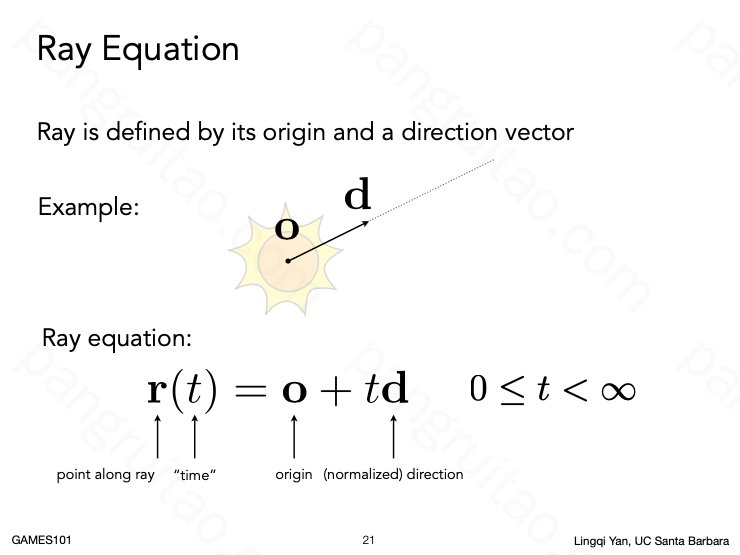
首先定义光线为一根射线
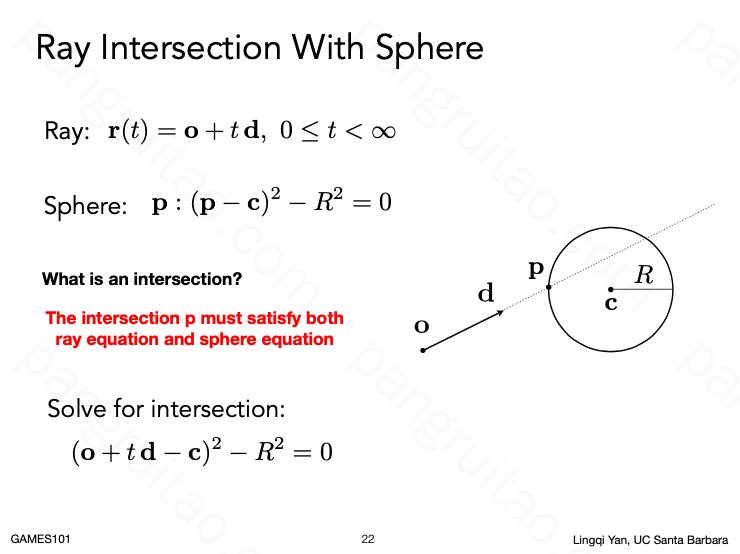
相交意味着两个方程有解
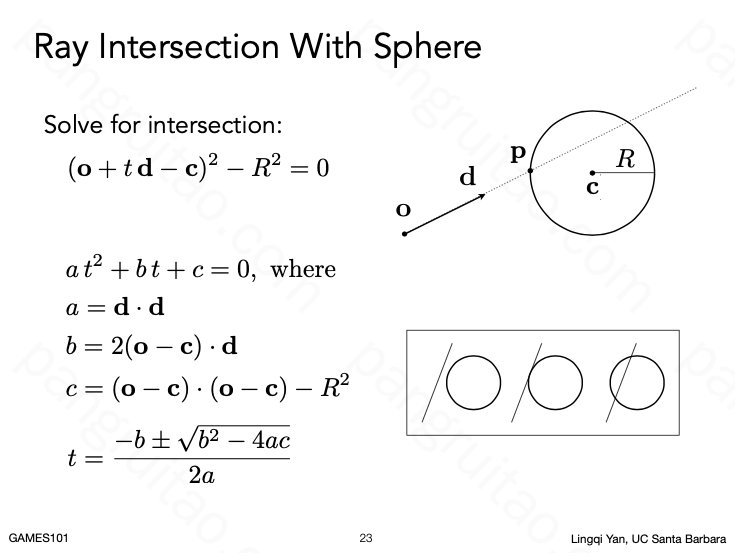
射线和球的交点是比较好求的

进一步推广到射线和其他表面的交点。求解通常用数值的方式,不需要把表达式求出来即可得到数值结果。

如果对于一个 Mesh 物体,则需要判断光线与各个三角形的交点。
这又有两个明显的问题:
- 如何求射线与三角形的交点
- 一个场景,甚至一个 Mesh 都可能有非常多的三角形,每次光线折射都需要全部求一次计算量过大,如何优化
首先,对于第一个问题,可以进一步分解成两步:
- 求射线与三角形所在平面的交点
- 判断交点是否在三角形内部
第二个问题则主要诉诸数据结构中的搜索树,以优化查询复杂度,详见后文

先求射线与三角形平面的交点,再求交点的重心坐标,根据坐标的正负性判断在三角形内或外,这是常用的思路。
而 Moller Trumbore 是一种简化后可快速求射线与三角形所在平面交点的重心坐标的方法
13.4 Accelerating Ray-Surface Intersection

有些场景的面数非常高,每次都求光线与每个面的交点导致的计算量会非常恐怖。

一种加速方式是给每个物体加上包围盒。
碰撞判断时首先判断是否和包围盒碰撞,如果有碰撞再检测和其中的三角形是否碰撞。
这样可以使没碰撞到包围盒的物体的检测次数降低至一次。
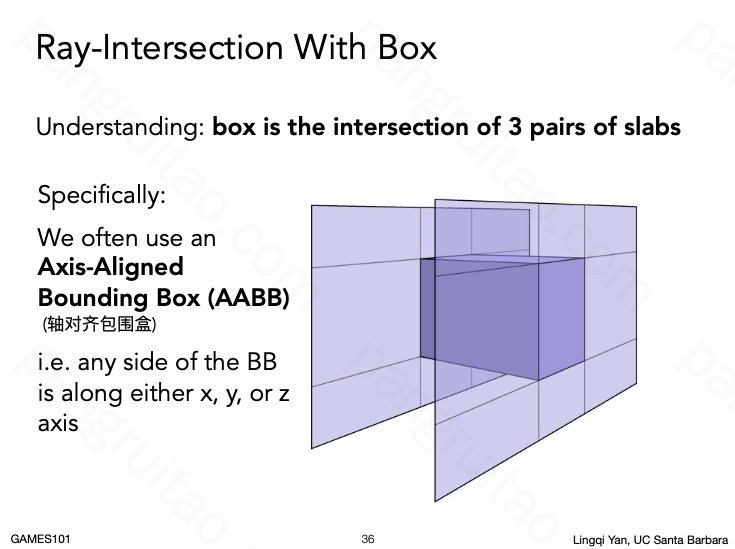
包围盒的碰撞检测方式是求射线与三组平行平面的交点

对每个平面求得与射线的交点之后进行裁剪(即取解集的交集),以获得最终结果。
如果裁剪之后没有位于包围盒以内的线段则意味着不相交。

当射线与与三组平行平面都有相交时,则与包围盒相交。

由于是求射线与平面的交点而不是直线与平面,所以需要考虑解的符号,进行特殊判断。
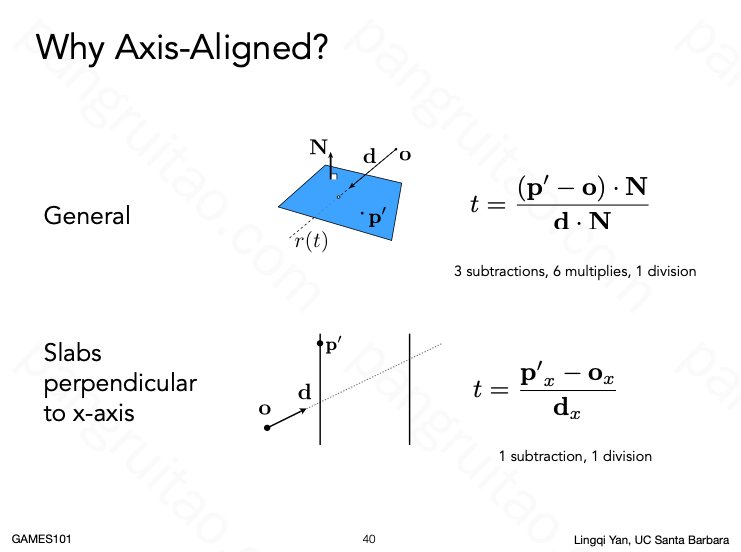
之所以尽可能使用与坐标轴对齐的包围盒主要是为了节省计算量。
14.Ray Tracing 2
14.1 Uniform Spatial Partition(Grids)
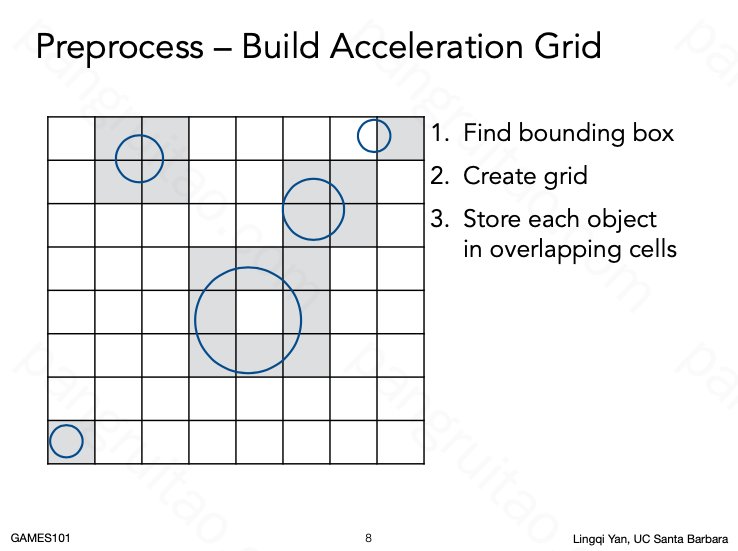
对空间进行均匀的网格划分,将物体注册到所占的空间中的格子。
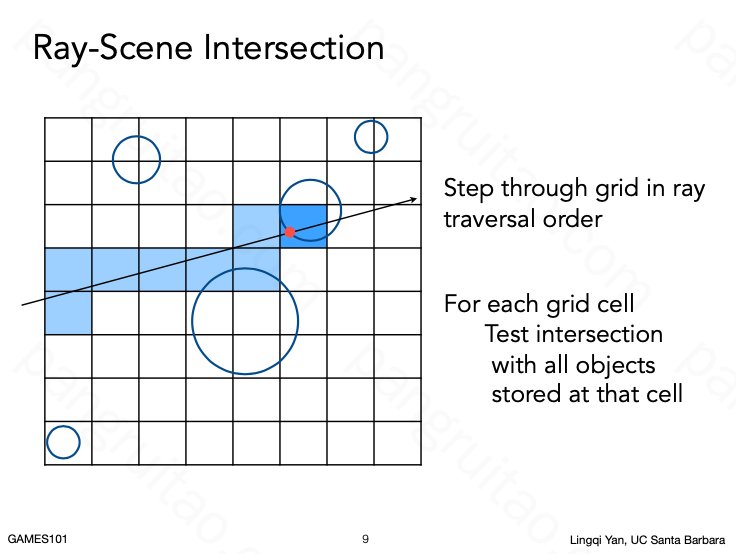
探测时仅检测光线与当前所在格子的物体是否有碰撞即可,减少检测总量。
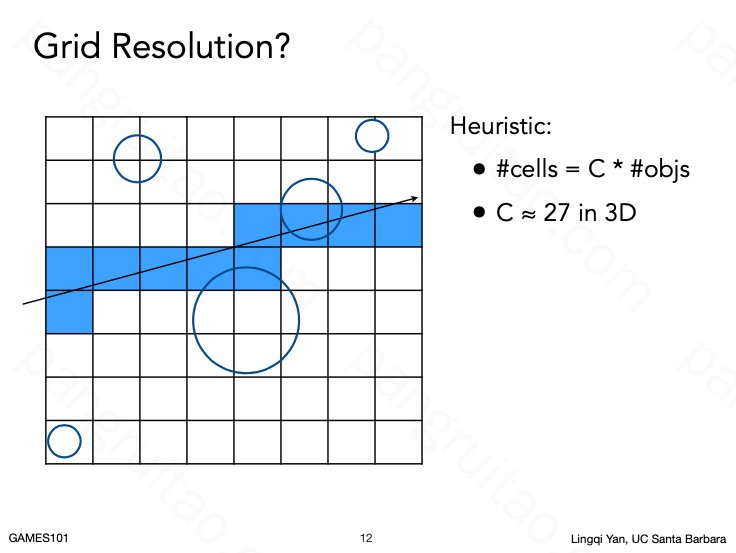
格子过密或者过梳都可能出现问题:
- 过密导致检测总量依旧偏多,需要花费大量计算于格子的定位和检测
- 过梳则导致一个格子包含太多物体,可能和不划分格子没有差异
所以一个经验公式是:格子的数量=27*物体数量

网格优化方式对于物体较小且分布较均匀的场景比较有效。

但对于物体大小差异很大的场景则优化效率非常有限,甚至反而增加计算总量
14.2 Spatial Partitions(Trees)
于是另一种方式是非均匀的空间划分
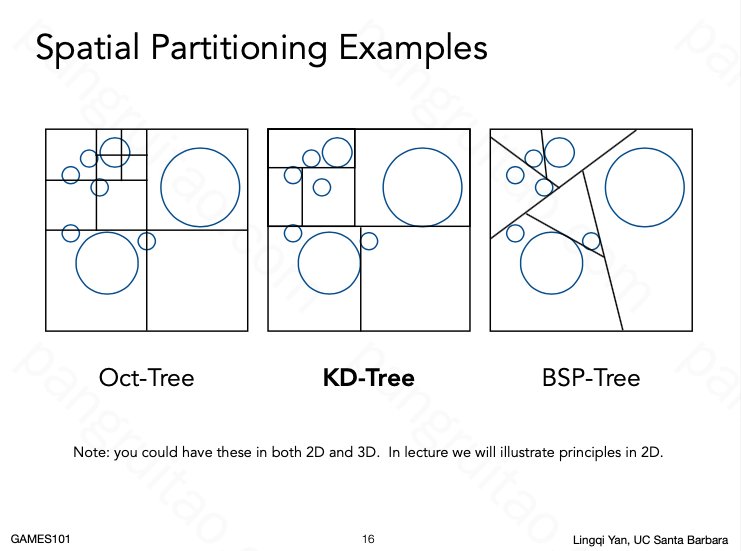
对此也有几种划分方式,本质都是构建搜索树:
- 八叉树对空间均匀划分,且在某种条件下停止划分(比如格子里的物体小于等于1个)
- 缺点是在一些应用中需要对高维空间进行划分,会导致每次划分出 \(2^n\) 个子节点,略爆炸,所以一般不倾向于用八叉树。
- KD-Tree 对空间进行动态的二分划分
- 每次轮流沿xy、yz、zx平面(可以相对均匀)对空间进行一次划分,不需要均分。整个结构类似于二叉树。且可以通过算法找比较好的划分位置,使物体尽可能少地跨越多个格子
- BSP-Tree 类似 KD-Tree 的二分方法,但允许不延轴向平面。
在图形学中 BSP-Tree 会导致判断时计算量相对于 KD-Tree 更高(前面的 AABB 判断),所以一般更倾向于使用 KD-Tree。
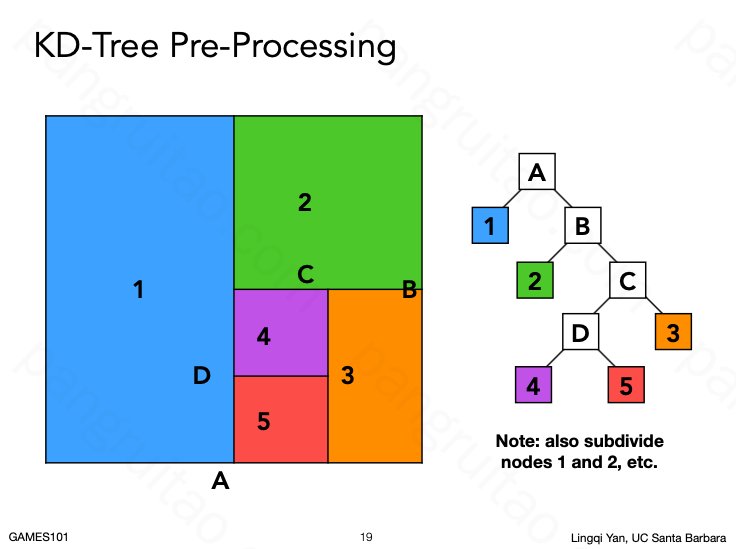
KD-Tree 的处理即不断循环找一个轴向平面对空间进行划分。得到一个二叉树。

其数据结构如上
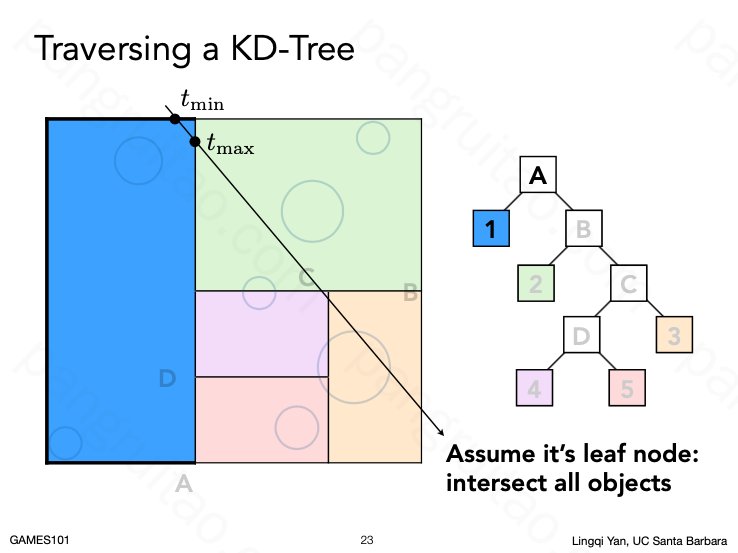
碰撞检测时,用类似AABB的方式不断求交定位节点,如果有子节点则进一步求交即可。
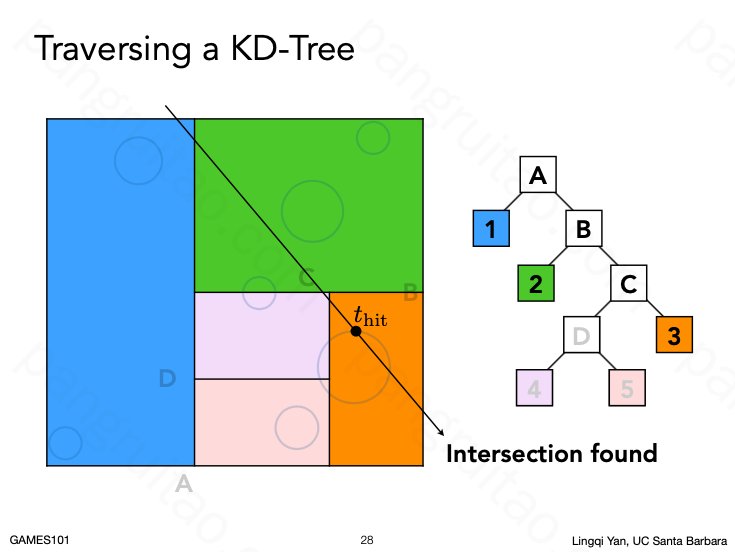
最后找到叶子节点中的物体进行相交判断,得到最终结果。
14.3 Object Partition:Bounding Volume Hierarchy
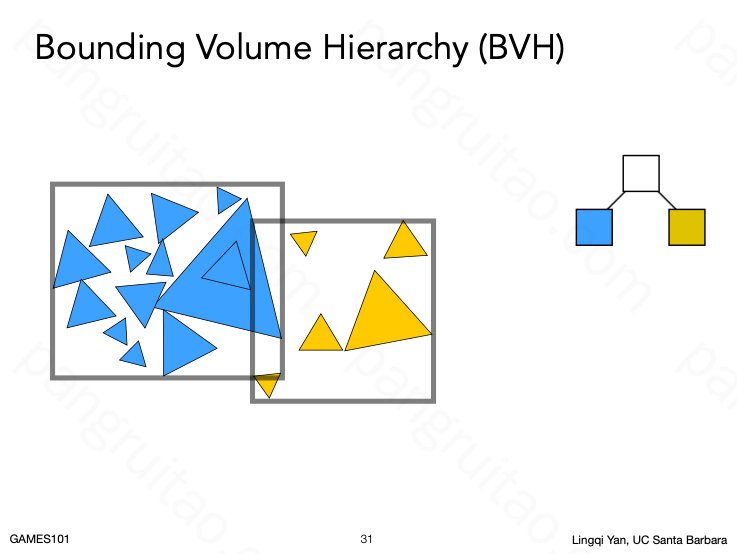
对三角形集的包围盒进行对象划分,每次也划分出两块,得到一棵二叉树。
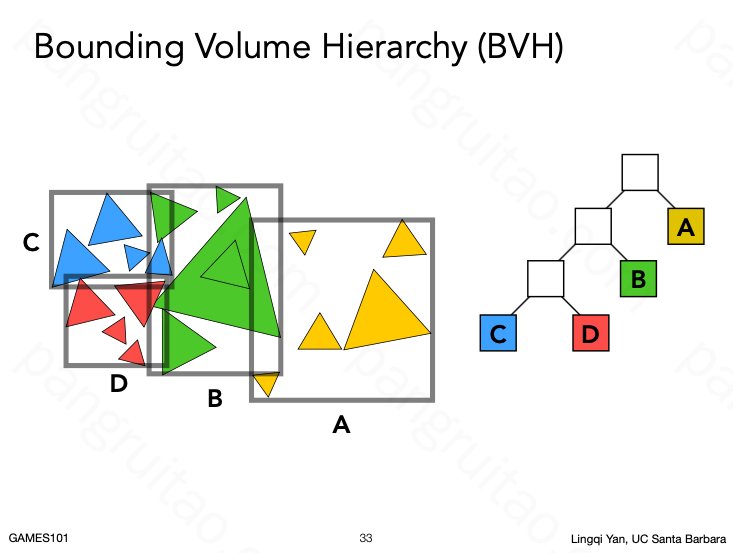
对一个节点进行多次划分的情况
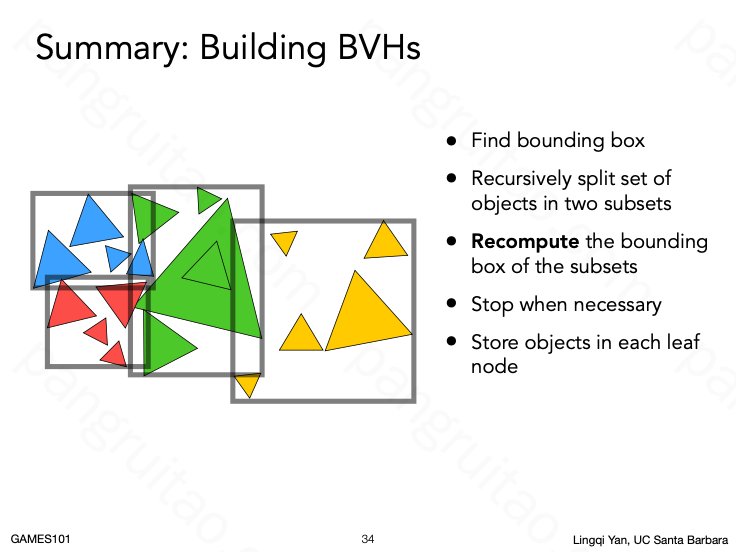
划分的过程总结

每次划分的一些原则

BVH 的数据结构
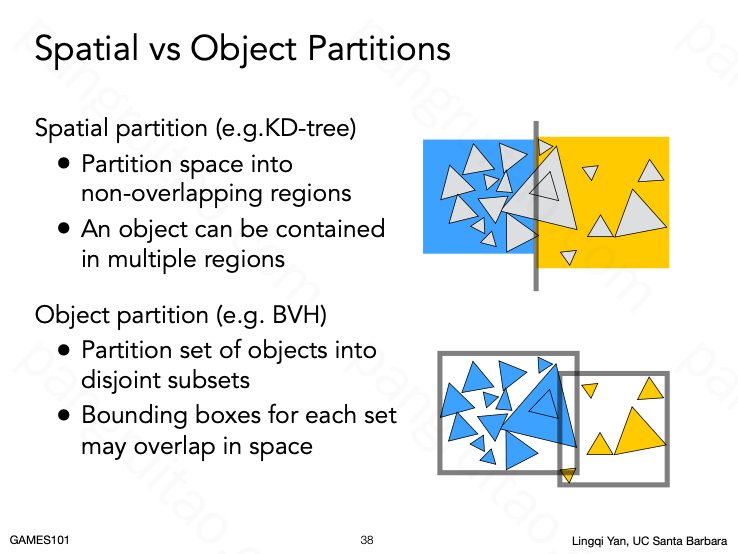
对空间划分和对对象两种方式性质的比较
14.4 Radiometry:Motivation

如果想使渲染效果尽可能地符合现实世界。
则需要研究现实世界的光的性质和传播原理。
也由此需要学习辐射度量学。
14.5 Radiometry:Energy and Flux

Radiant 是辐射能量
Radiant Flux 是辐射强度,单位为瓦特。
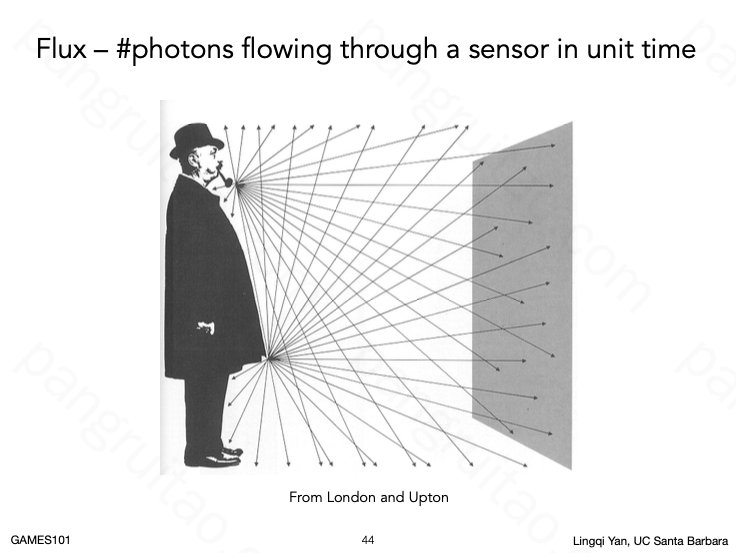
Radiant Flux 也可以理解为单位时间通过单位平面的光子数量。
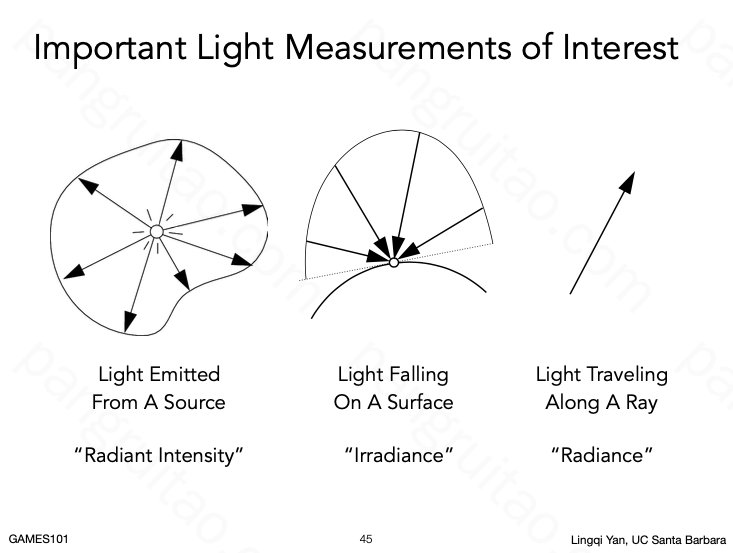
三种复合的光线度量:
- Radiant Intensity:一个光源的辐射强度(单位 坎德拉 Candela 或 流明/单位角)
- 度量某角度上的 Radiant Intensity 有一个单位是 流明=坎德拉*球面度。
- Irradiance:一个点接受的辐射强度(单位:流明/平方米)
- Radiance:一根线上的辐射强度(单位:nit 或 流明/单位角/平方米)
14.6 Radiometry:Radiant Intensity
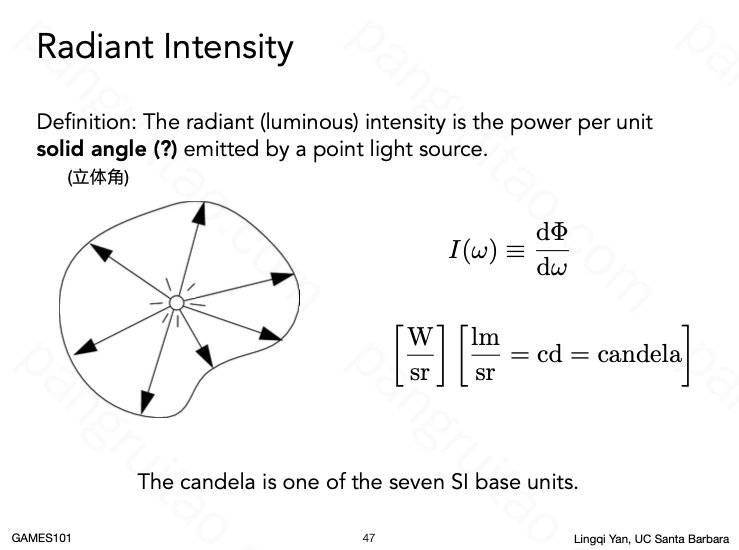
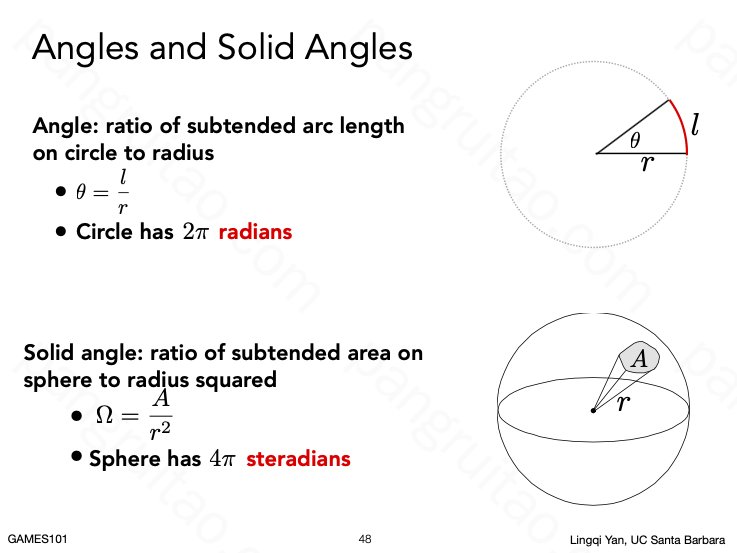
立体角的定义或计算方式。(这也可以看出弧度相对于角度的好处:可以容易地往高维推广)
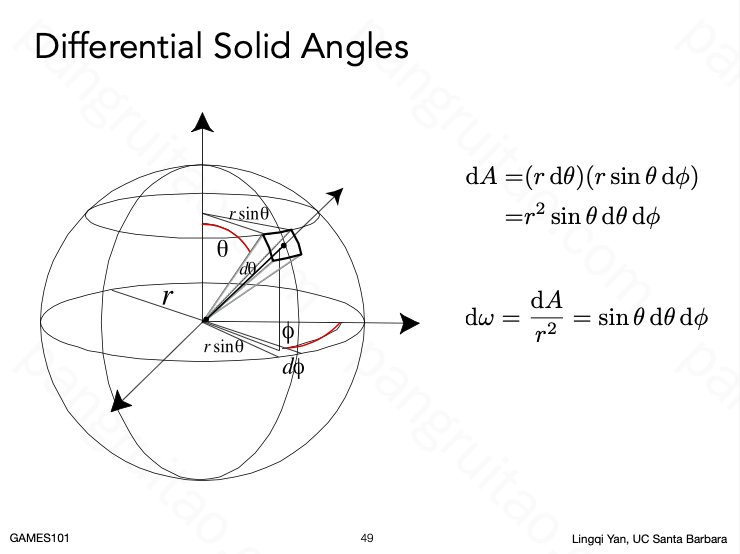
立体角的微元,即球面的微元
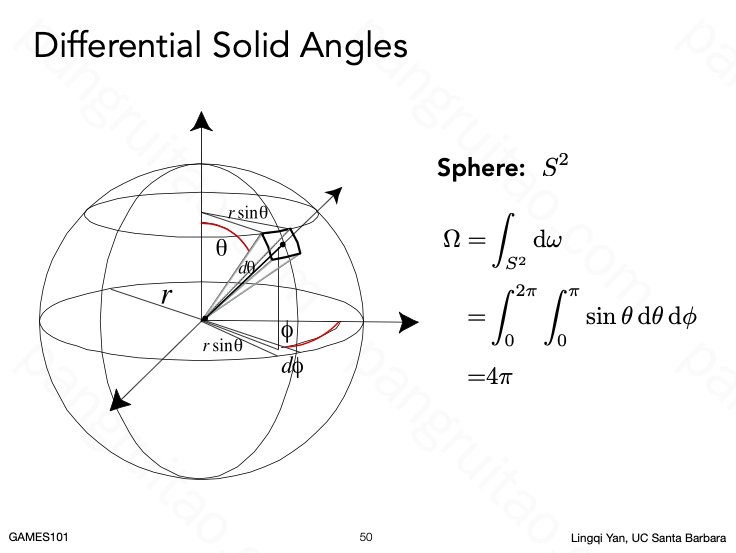
完整空间的立体角即单位球的表面积 \(4\pi\)
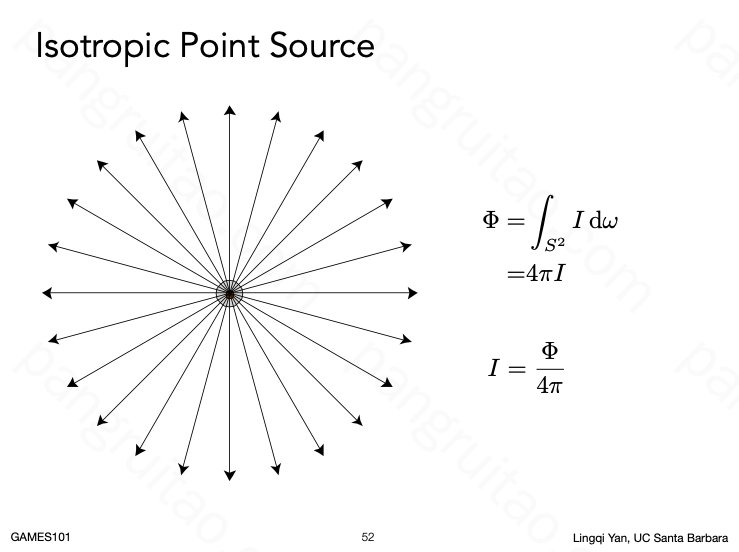
因此对于一个各向同性的点光源而言:
Radiant Flux=Radiant Intensity * \(4\pi\)
或者 Radiant Intensity = Radiant Flux / \(4\pi\)

而 Radiant Flux 对应度量单位 Lumen(流明)。由此可知一个 815 流明的灯,如果向各个方向辐射的强度一致,其 Radiant Intensity 即 65 坎德拉。
15.1 Radiometry:Irradiance
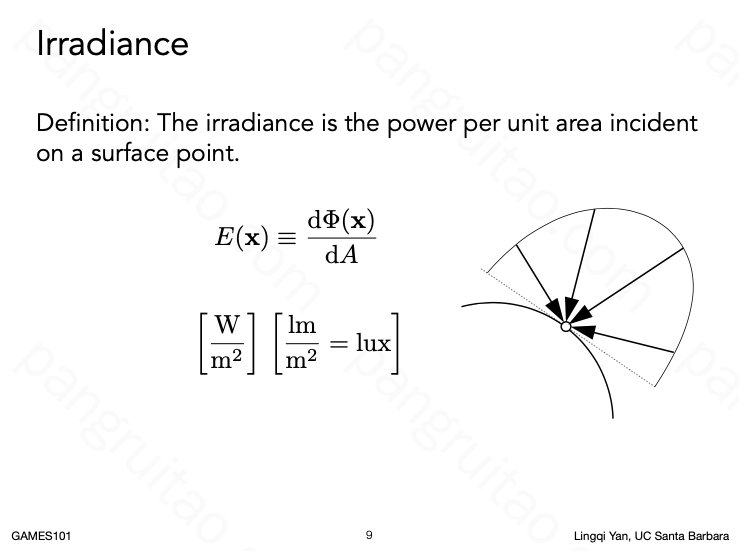
Irradiance 即辐射强度在面积上的强度
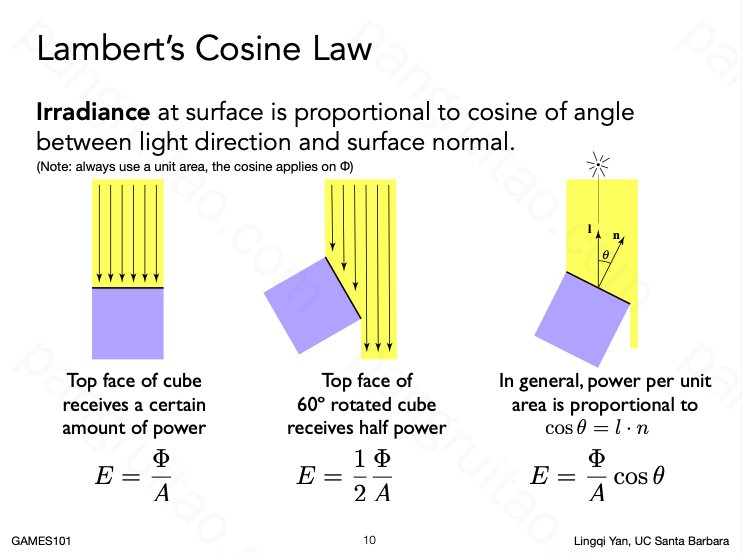
基于此可以容易知道在光栅化的 Lambert 渲染方式中 cos 的物理意义。

同时一个杂知识:春夏秋冬温度变换不是由于地球公转离太阳远近,而是由于地球自转轴相对于黄道平面的偏角导致南北半球随公转接受的 Irradiance 也跟着变化,进而有了春夏秋冬。
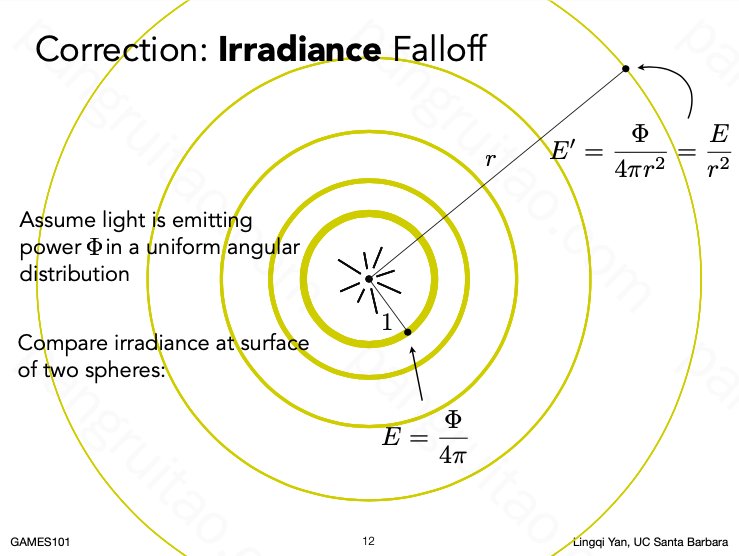
Irradiance 是会随着距离平方反比进行衰减的(即使不考虑介质吸收的能量)
15.2 Radiance

Radiance 是描述光线在环境中传播最基础的量。
渲染基本上就是在计算 Radiance

Radiance 是 Radiant Intensity 在面积上的微分
Radiance 也是 Irradiance Intensity 在球面角上的微分
其单位为 nit

