GAMES101(15-16):光线追踪下-学习笔记

GAME101笔记汇总

GAMES101:汇总-学习笔记

15.Ray Tracing 3

15.1 BRDF

图形学中，当我们想描述一个材质，其实就是在描述此材料和光线的作用方式。

BRDF 全称 Bidirectional Reflectance Distribution Function。是一种描述材料表面和光进行反射作用相关的方式的函数。

在熟悉 Radiant Intensity、Irradiance、Radiance 几种概念（详见光线追踪上）之后，便可以基于概念这些对材质和光的作用进行略精细的描述了。

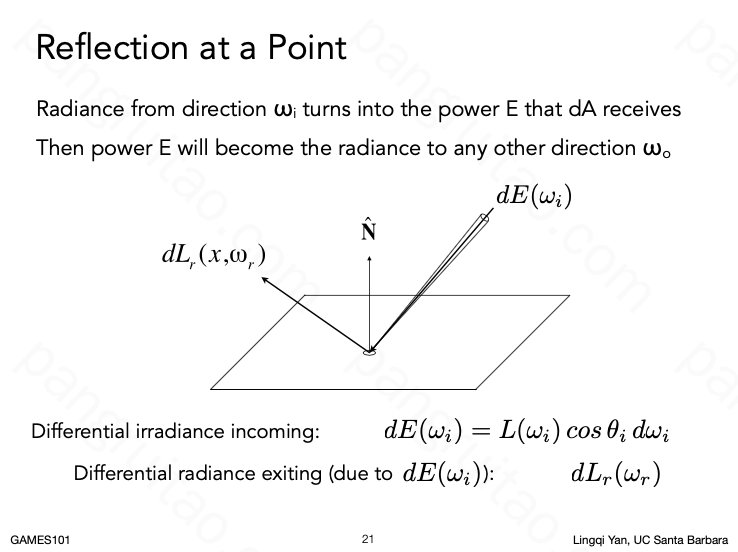
首先考虑表面上一个面积微元的反射情况：如果我们知道任一方向的入射光或反射向任意方向作为出射光的比例，也就知道了其表面的反射性质。

由此可以定义一个函数 \(f_r(\omega_i \to \omega_r)\) 描述入射方向到反射方向的反射能量比例。其单位是 1/立体角

15.2 The Rendering Equation

由此，如果想求得某个点沿某个出射方向的总功率，则对其各个入射方向反射至此出射方向的能量进行积分即可。由于这里还只考虑反射，不考虑折射，所以积分集合通常是上半球。

当然，光线并不会只反射一次，所以通常还需要递归进行计算光的强度。

如果在考虑反射的同时，再考虑上其自发光的性质，则再加上一项 \(L_e(p,\omega_o)\) 进行自发光的描述即可。

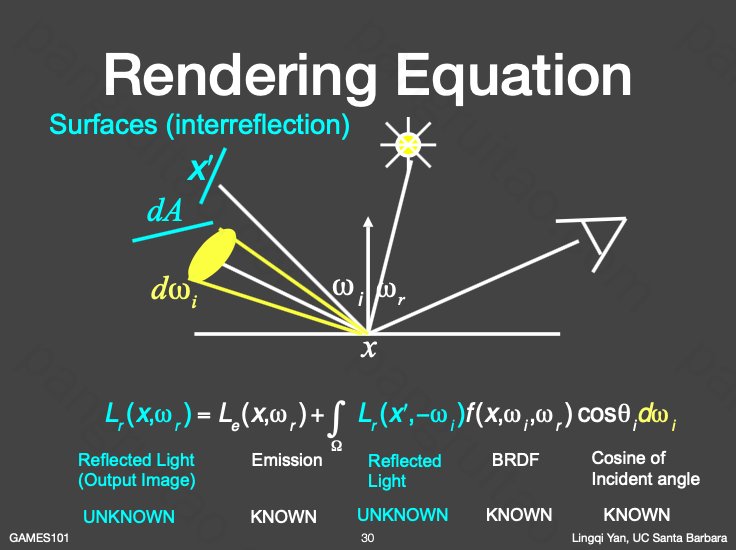
由此得到了“渲染方程”

对渲染方程每一项再一次进行梳理

如果是求离散点光源的场景，还可以不用积分，直接加和求解即可。

如果某一个光源是面光源再对其使用对面积的积分

光源也可以是一个表面反射出的光，毕竟反射的光和光源的光没有本质差异

用这种方式渲染出的场景效果

还可以对渲染方程的形式进行简化

甚至利用算子进一步简化渲染方程的形式

如果写成算子形式，可以做变换之后对其进行类似级数的方式展开。

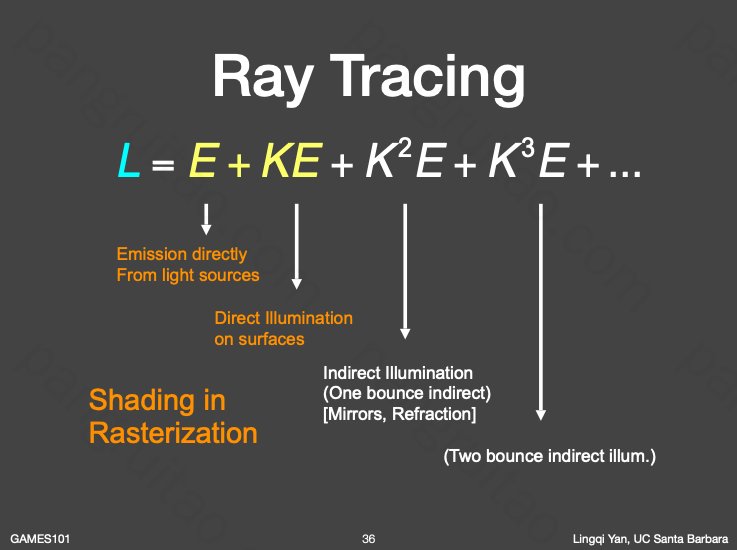
得到这样的一个渲染方程。

可以对其进行理解：最后的光照是直接光照加一次弹射加二次弹射…

其中直接光照和一个反射的光照是光栅化也可以做到的。但再想加上更多次的弹射，光栅化实现就比较困难了。因此需要光线追踪。

一个例子：

只考虑直接光照，即光能够直接达到的地方有颜色，否则黑色（如p点）

考虑一次弹射

考虑四次弹射（四次弹射才保证了光能够穿过灯，所以此时灯才亮起来）

十六次之后整体变化已经不大了，通常可以对这种“变化度”进行度量，在合适的情况下停止进一步计算。

16.Ray Tracing 4

16.1 Monte Carlo Integration

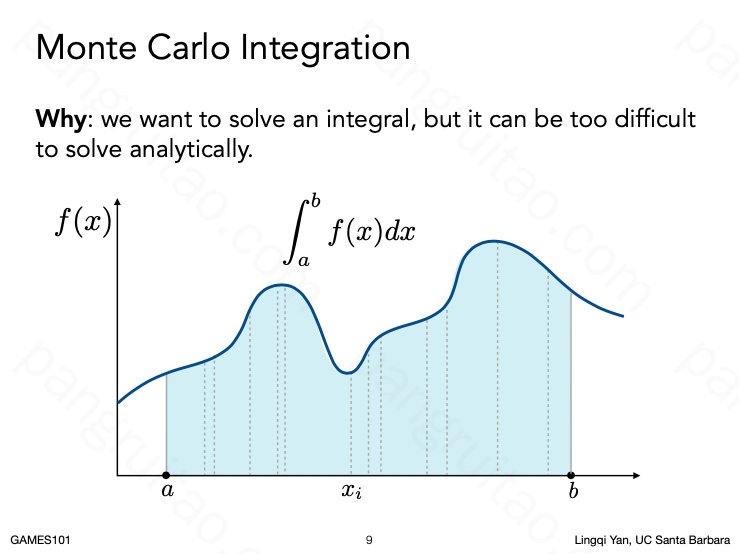
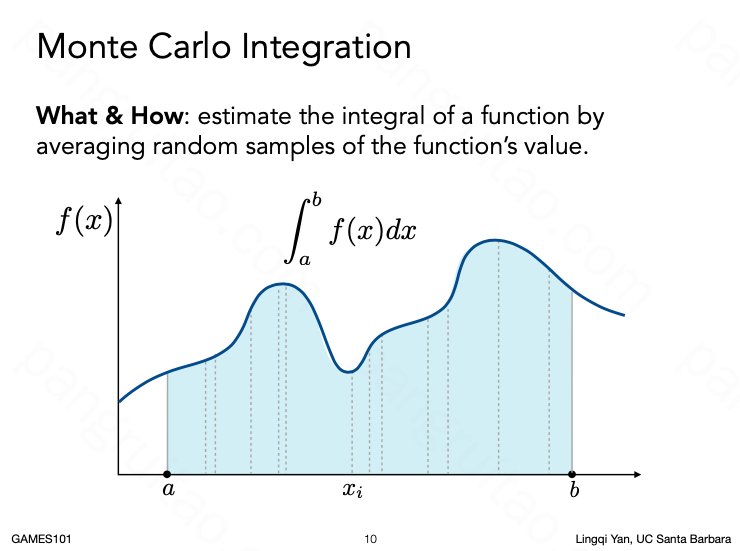
有些积分如果用解析的方式非常难求

蒙特卡洛提供了一种很好的近似方法

使用蒙特卡洛积分对一个均匀分布的函数进行积分

16.2 Path Tracing:Why

Whitted-Style 的光线追踪是做了一些近似和省略的，会导致一些问题，比如

毛糙的反射表面的效果无法达到

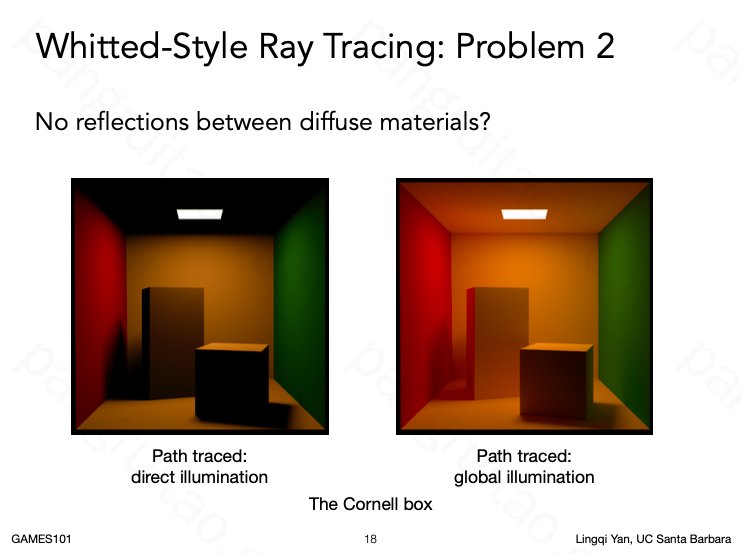
没有多次反射而造成的渲染的问题

如 Whitted-Style 那样简化会产生问题

但如果像渲染方程那样求解又会面临至少两个明显的大问题：

1. 需要求解一个函数在球面上的积分
2. 需要递归处理

对于第一个问题，由于我们只需要数值解，于是可以应用蒙特卡洛积分方法

对于第二个问题，由于我们已经知道光线是可以由直接光照+一次反射+两次反射+….构成，于是可以按这个式子一项一项求。并且现实经验下这个式子虽然无限长，但是是会收敛的（否则我们眼睛看到的画面应该随时处于过曝状态），因此一项一项求，并且在合适的时候舍弃后面的项是合理的。

16.2 Path Tracing:What and How

用蒙特卡洛积分求解渲染方程

写成伪代码还挺简单

如果进一步考虑全局光照呢

则加上递归的反射计算

但仅仅这样是不够的

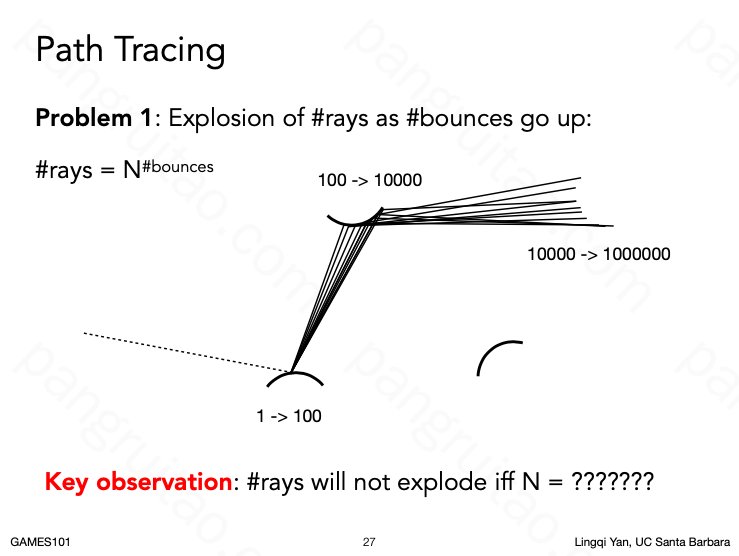
仅这样的话，运算量会爆炸

Path Tracing 的方法是仅仅考虑一根光线

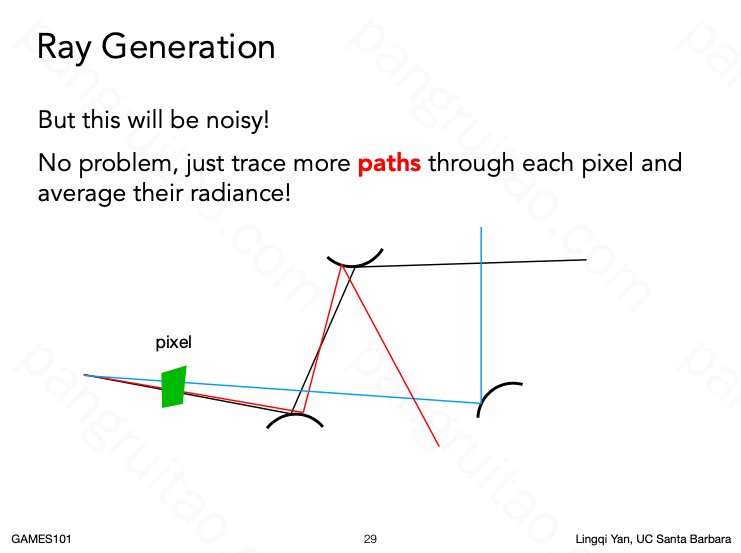
但考虑多个路径

这样可以避免运算量爆炸

最后把每个路径得到的渲染值加起来求平均得到像素的值

与此同时，还有一个问题，即需要结束递归

通常采用俄罗斯轮盘赌的方式（指数分布）指导递归次数

并且次数的期望值也是容易控制的

由此综合起来路径渲染函数的伪代码如上

这样做以后已经保证了有效性，但并不保证收敛效率，次数较低时噪点可能很多，特别是对于光源比较小的场景而言。

这背后的原因是大量的光线没有到达光源，这些计算都被浪费了。

对于这样的问题，一种处理思路是蒙特卡洛积分时由从整个半球上采样改为从光源表面（也可以是反射物体表面）上均匀采样，这样得到的所有光线都一定不会被浪费。

但这样也会导致一个问题：蒙特卡洛积分要求采样是在自变量积分区间，而非其他区间，所以还需要一个变换

加上一个投影系数

得到新的方程

这样做了之后，采样的光线将准确地来自于光源或者其他物体，提升了采样效率

这样修改后，路径追踪的算法基本已经完成

并且路径追踪算法的效果非常好，几乎已经达到了和真实的照片一致的效果

光线追踪除了以前的 Whitted-Style 和现在的 Path Tracing，还有Photon Mapping等等方案。

当然，对于 Path Tracing 还有一些问题没有说清楚，但都有各自的解决方案