1.不等式内容
设随机变量 \(X\) 具有数学期望 \(E(X)=\mu\) ,方差 \(E((X-\mu)^2)=\sigma \),则对于任意正数 \(\epsilon\) ,成立
\begin{align}
P{|X-\mu|>\epsilon}\leq \frac{\sigma^2}{\epsilon^2}
\end{align}
2.证明
考虑任意 \(X\) 的概率密度函数 \(f(x)\) :
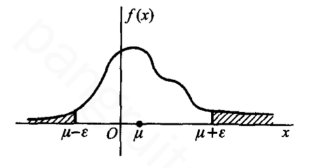
对随机变量 \(X\) 其方差满足
\begin{align}
\sigma^2 &= E((X-\mu)^2) \\
& = \int_{-\infty}^{\infty}(x-\mu)^2f(x)dx \\
& = \int_{-\infty}^{\mu-\epsilon}(x-\mu)^2f(x)dx + \int_{\mu-\epsilon}^{\mu + \epsilon}(x-\mu)^2f(x)dx + \int_{\epsilon +\mu}^{\infty}(x-\mu)^2f(x)dx \\
& \geq \int_{-\infty}^{\mu-\epsilon}(x-\mu)^2f(x)dx + \int_{\epsilon + \mu}^{\infty}(x-\mu)^2f(x)dx \\
& \geq \int_{-\infty}^{\mu-\epsilon}\epsilon^2f(x)dx + \int_{\epsilon + \mu}^{\infty}\epsilon^2f(x)dx \\
& = \epsilon^2 (\int_{-\infty}^{\mu-\epsilon}f(x)dx +\int_{\epsilon +\mu}^{\infty} f(x)dx) \\
& = \epsilon^2 P \{ |X-\mu| \geq \epsilon \}\\
\end{align}
于是得到
\begin{align}
P\{|X-\mu|>\epsilon\} \leq \frac{\sigma^2}{\epsilon^2}
\end{align}
或
\begin{align}
P\{|X-\mu|<\epsilon\} \geq 1- \frac{\sigma^2}{\epsilon^2}
\end{align}
3.应用
由于不等式的要求非常宽松,于是对任意奇葩分布都可以在已知期望和方差的情况之下,得到关于期望值对称的区间的概率下限(或此区间外的概率上限)。