GAME101笔记汇总
1.Overview of Computer Graphics
对课程内容进行大致介绍。同时对图形学进行介绍。


大牛的成就

介绍一下图形学是什么,以及为什么学图形学
之后介绍了课程包含的四大内容:
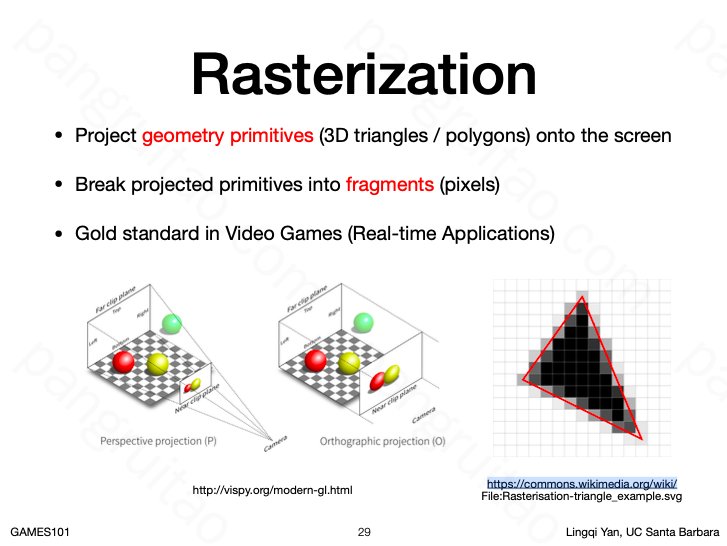
光栅化
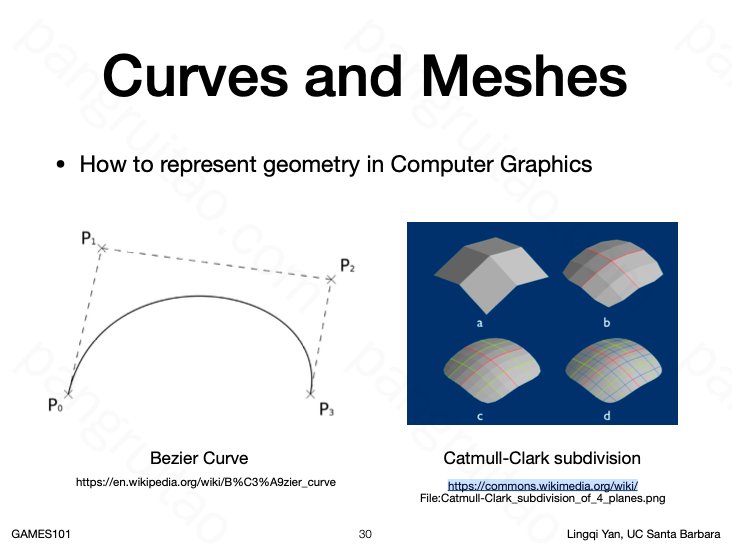
几何

光线追踪

动画和仿真
2.Review of Linear Algebra
这节课主要回顾了一下线性代数相关的基础知识,包括向量、向量运算、矩阵、矩阵运算等等。基本在本科覆盖范围内,因此叫 Review
3.Transformation
3.1 Basic of Transformation
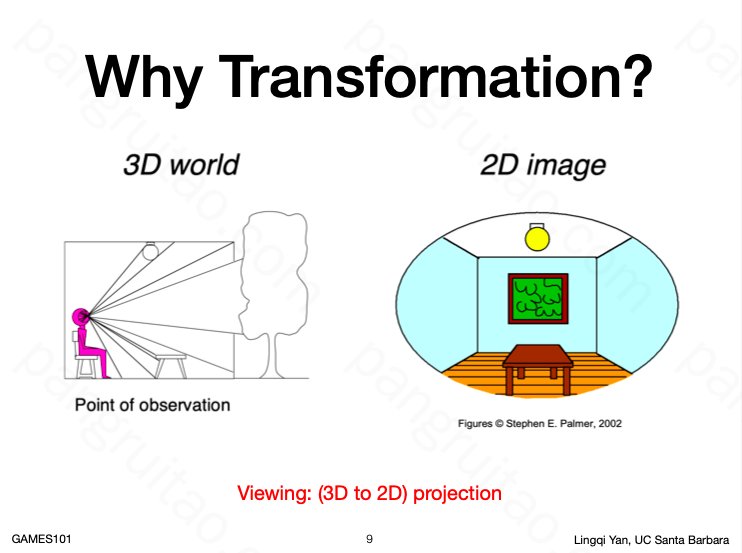
首先用几个例子(摄像机在空间中的运动、机器人运动、视角变换)介绍一下为什么要用 Transformation
之后介绍几种二维上的基本变换
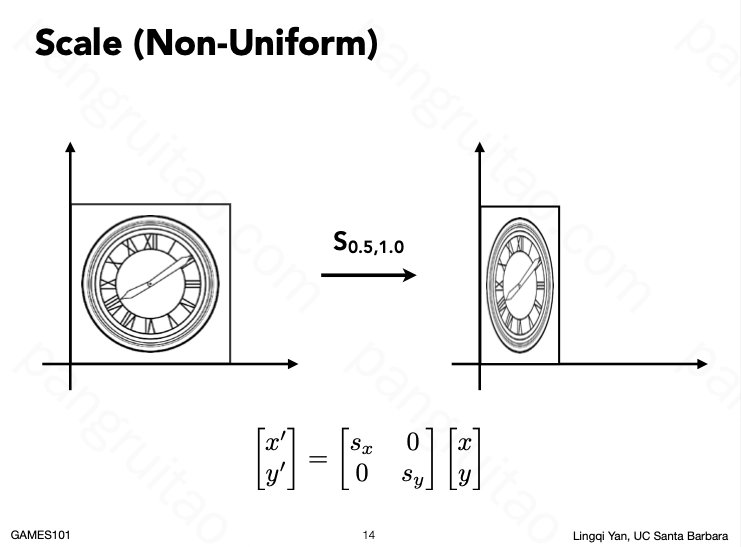
缩放变换
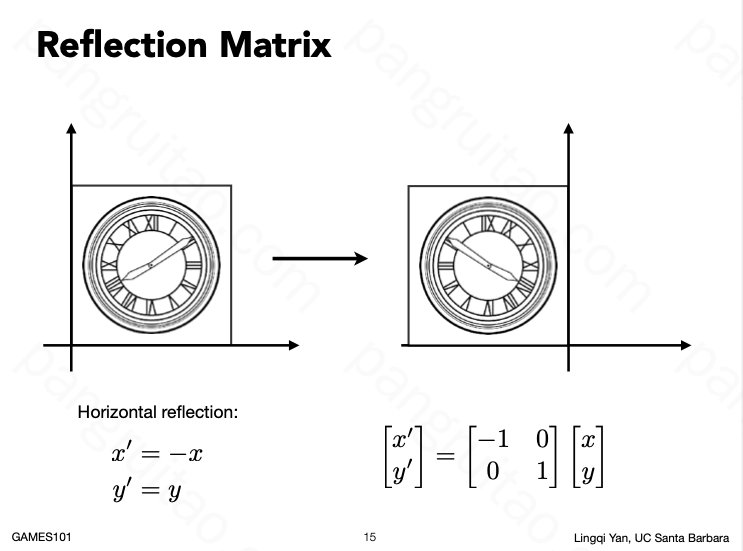
镜像变换
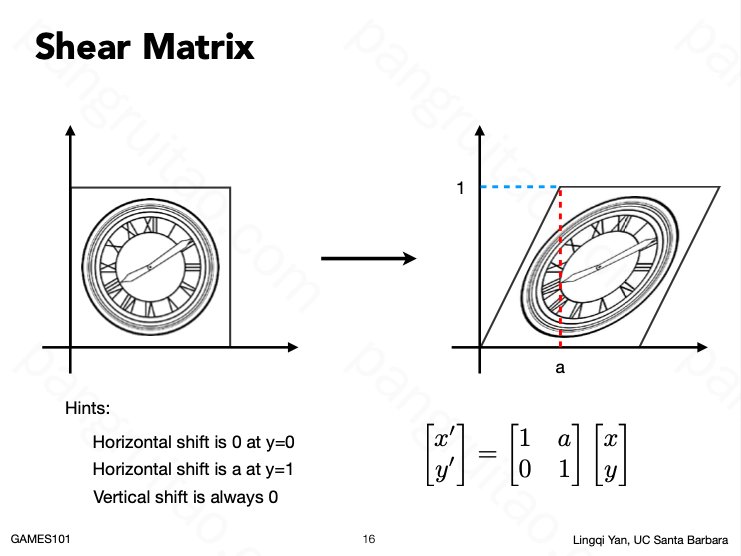
切变
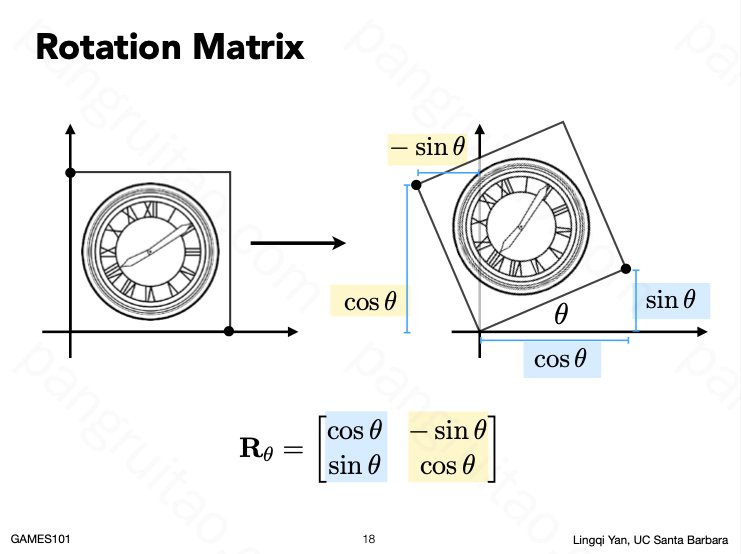
旋转
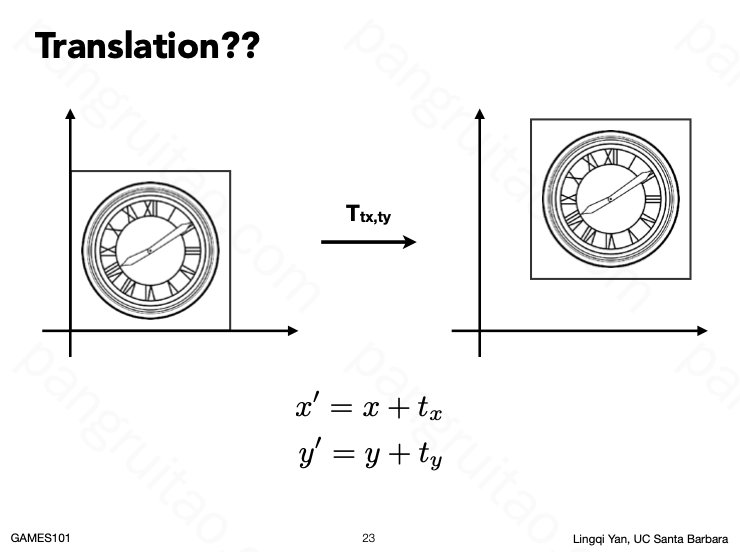
平移变换,但通常在齐次坐标下进行。
合在一起成为仿射变换

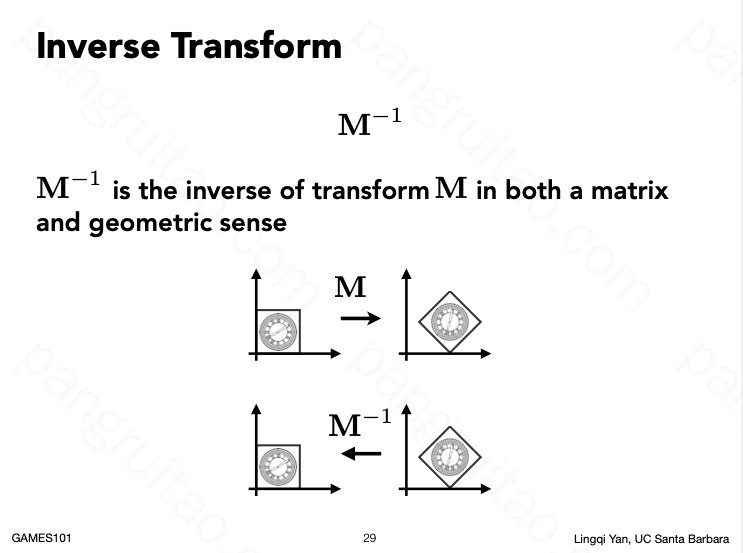
逆变换即逆矩阵

基本变换组合为符合变换
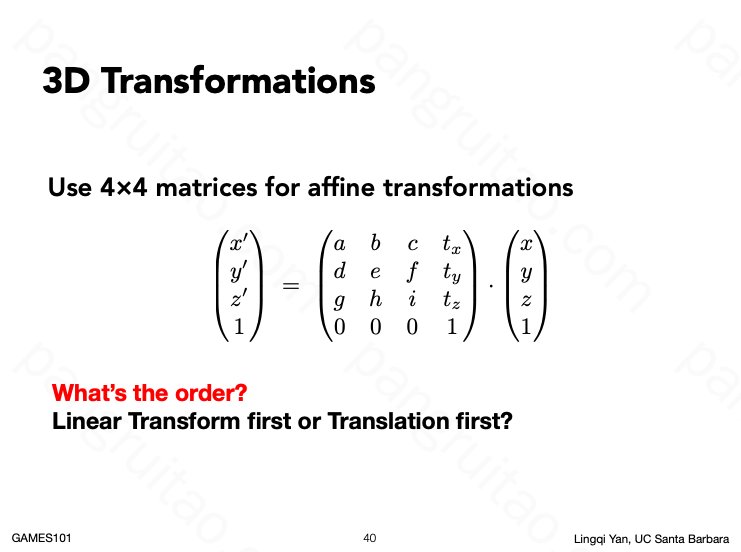
再升级看三维下的坐标变换
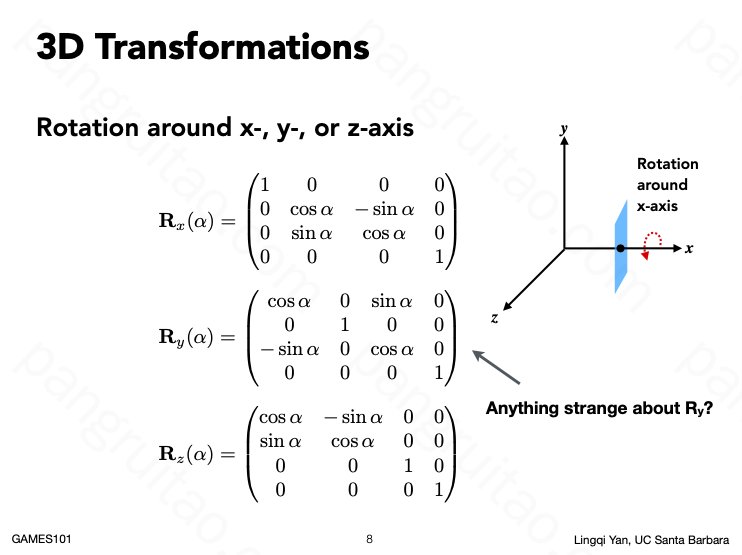
3D 的缩放、镜像、切变基本和 2D 可直接类比。但是旋转会有一些麻烦。这是一种解决方案,将任意旋转分解为绕坐标轴旋转。
并且这里需要注意坐标系,课程中使用的是右手坐标系,部分API和软件会使用左手坐标系

绕任意轴旋转的方程
接下来考虑视图或摄像机的变换
3.2 Camera Transformation

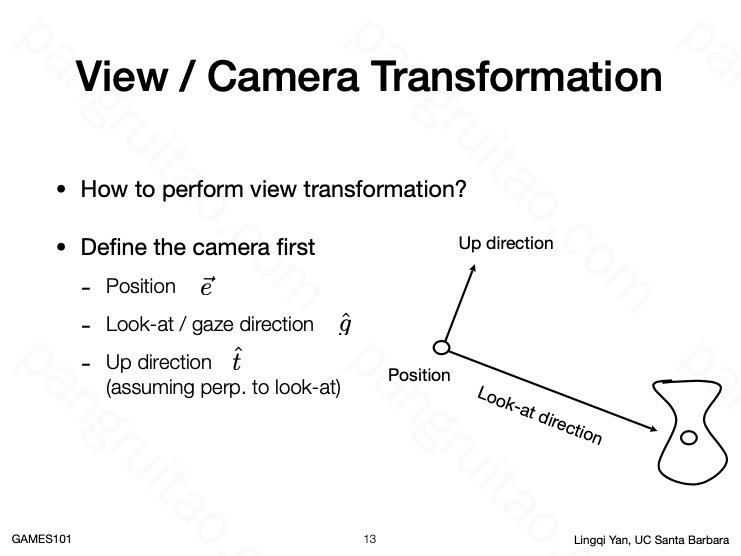
三维摄像机有 7 个维度
- 位置:3维
- 朝向:3维
- 画面旋转:1维
通常用三个向量进行对应
- 位置向量
- 朝向向量
- 上方向量(由于一定和朝向正交,所以会冗余2维)
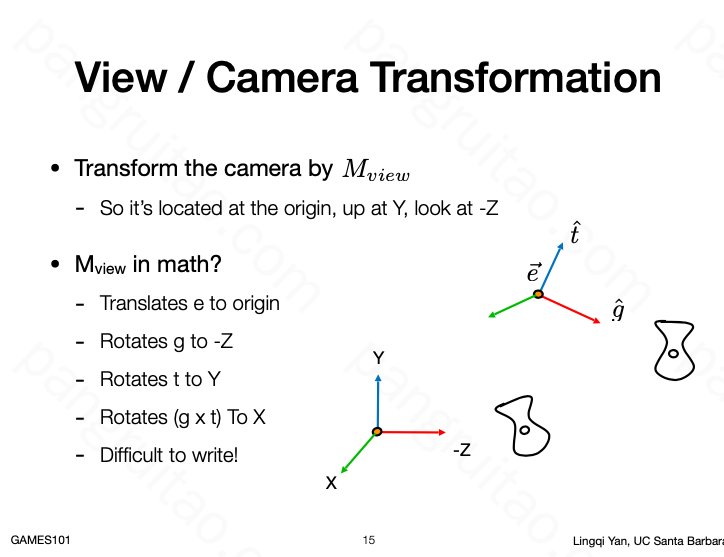
正向考虑 摄像机变换 的矩阵是比较麻烦的一件事情

但反向考虑则比较容易,所以可以通过反向考虑,配合矩阵求逆得到结果。
4.Transformation
4.1 Projection Transformation
投影变换本身是一个降维变换,图形学中主要针对于将三维投影至二维
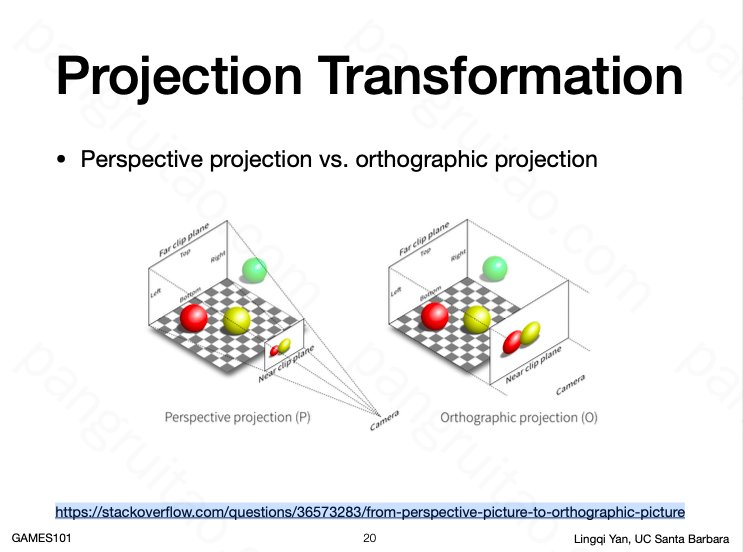
3D 至 2D 的投影主要有两种:平行投影和透视投影
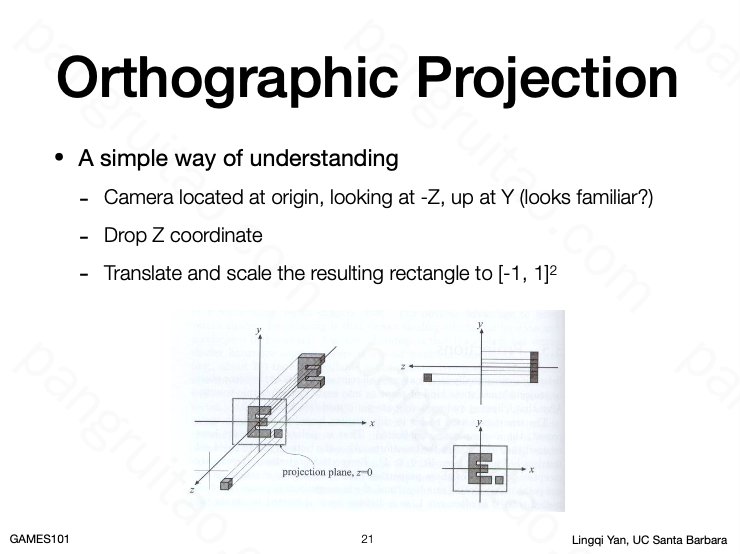
平行投影的操作比较简单,直接丢掉坐标中的 Z 分量即可。
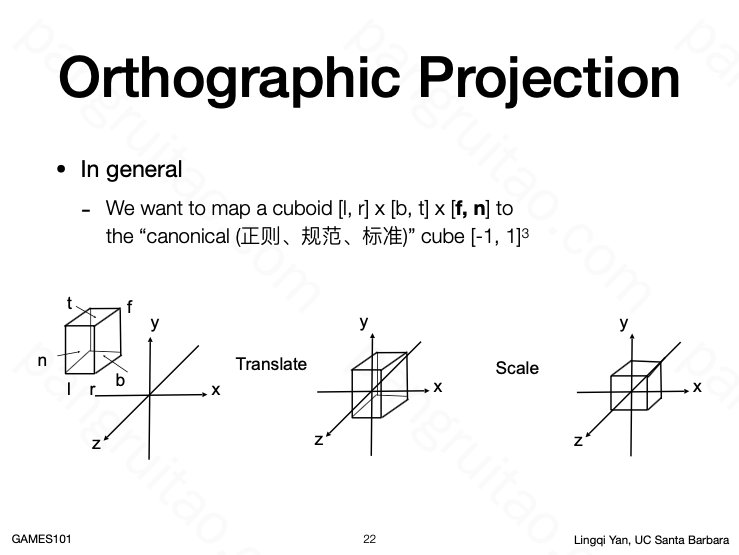
但通常需要 canonical ,即首先将视图空间中心平移至 原点,再缩放为标准正方体。
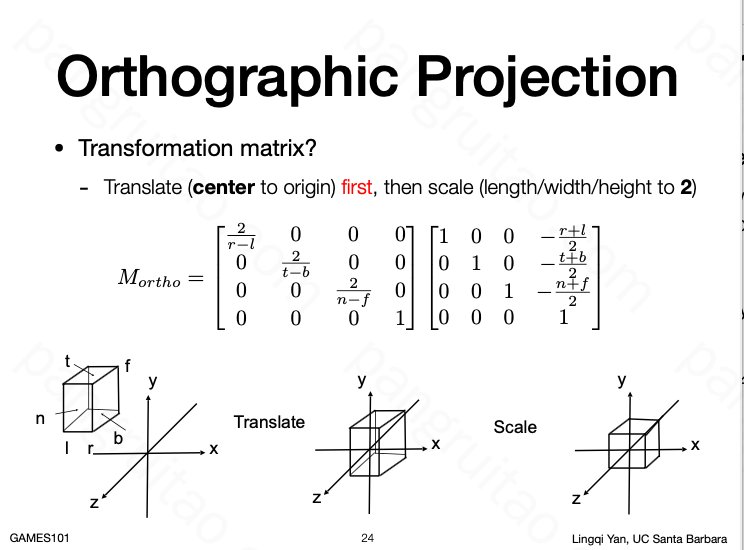
整理一下可知这一系列操作对应的矩阵。
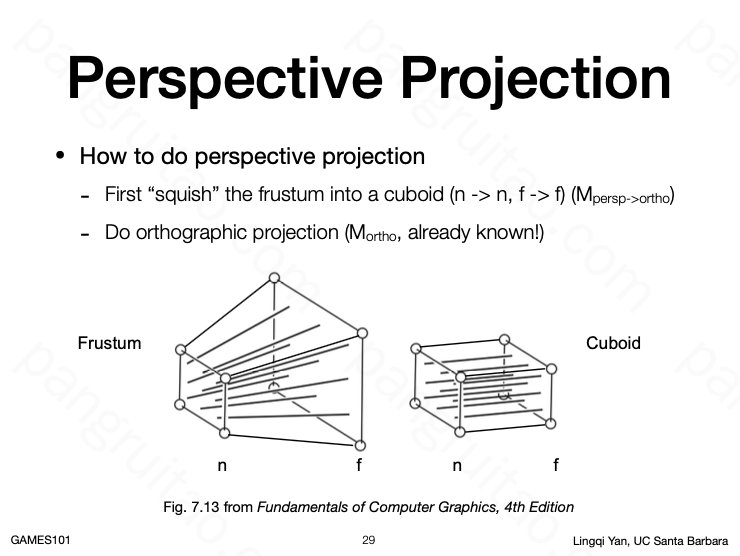
透视投影本质上是将空间投影至一个点,但在过程中用一个平面(如胶片)截下。
而对于透视变换,可以考虑将其先变换为平行,再用平行投影。
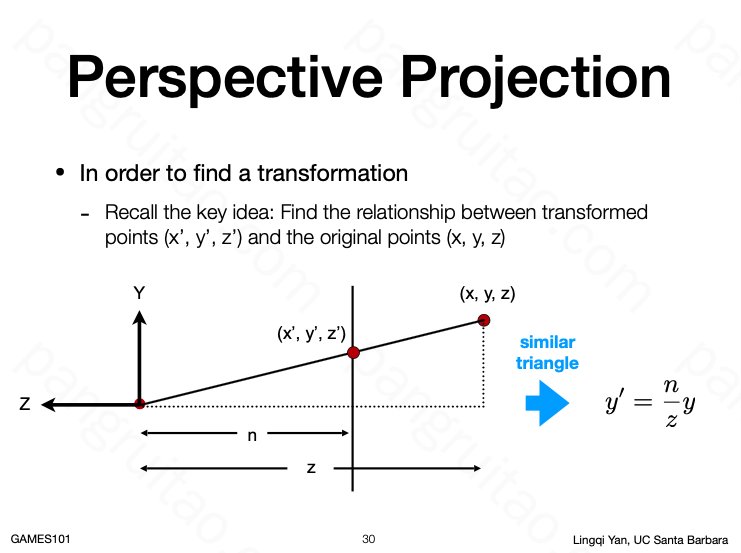
这个矩阵并不直观,但是可以通过设立条件对矩阵进行推导
- 胶片所在平面不发生变化
- 而远处的平面大小缩放至和胶片一样大,且中心对齐,但 Z 值不变
以此即可确定变换矩阵