主要梳理一下B树的插入和删除的方法和原理。
1. B树简介

又称多路平衡排序树
- B树需要满足几个要求
- 节点的最多子树数量为B树的阶,通常用m表示
- 对每个节点,子树数量 = 关键字数量 – 1
- 每个节点至多有 m 棵子树,节点内的排列为 一个子树、一个关键字、一个子树….一个子树,所以关键字至多 m-1。
- 子树可以为空
- 根节点以外,每个节点至少有 \(\lceil \frac{m}{2} \rceil\) 个子树,或 \(\lceil \frac{m}{2} \rceil – 1\) 个关键字。
- 所有叶节点出现在同一层上,且为空
- B树节点存储结构
- 一个整数记录节点中真实有效的关键字数量
- \(m-1\) 个关键字
- \(m\) 个节点指针
- (如果存在)关键字对应的内容,或对应的内容地址
2. B树元素的插入
2.1 找到插入位置
当需要插入新节点时,首先二分查找找到节点所在的最底端位置,查找方式与二叉排序树很接近。

2.2 最好的情况
如果插入后,对应节点的关键字总数 \(k + 1 \leq m\) 则意味着依旧满足要求,无需进一步调整。
2.3 节点分裂

一旦插入过后节点关键字数量超过了m上限,则可以用一个通用的分裂的手段进行操作:

即把自己一分为而,并且创建一个父元素,可以发现这种分裂行为下,子树的数量和顺序都没有受到任何影响,即无论对子树空或非空的节点都可以操作。
具体到前面的情况,则是把父元素插入以前的父节点对应位置:

如果父节点的关键字没有超m上限自然最好。如果超了,则对父节点采用相同的分裂手法继续往上递交元素。
如果没有父节点,则让父元素成为新的父节点,即新的树根,此时树的层数增加一。
3. B树元素的删除
3.1 找到删除的元素
首先在B树中找到想到删除的元素,如果这个元素所在节点不在最底层,则根据要求,一定有子树,则任意找到其前驱或后继,换一下位置用来代替他被删除,思路和红黑树里的代替方式几乎一致。
总之可以归约为删除非空的最底层节点元素问题。如我们找到了元素:

于是先直接删除元素。
3.2 最好的情况
如果被删元素所在节点原本的关键字数量 \(k\) 满足 \(k > \lceil \frac{m}{2} \rceil – 1\) 即 \(k-1 \leq \lceil \frac{m}{2} \rceil – 1\),这时树依旧满足要求,无需进一步调整。
3.3 找兄弟借
如果左或右兄弟(按要求除非是根节点,至少有一个兄弟)的节点元素数量 \(k\) 满足 \(k > \lceil\frac{m}{2} \rceil – 1\),则意味着借出一个也不影响满足要求,于是可以通过如下方式转移元素:

转移过后节点都满足了要求,并且顺序也没受到影响。
3.4 节点合并
当一个节点的元素数量为 \(\lceil \frac{m}{2} rceil – 2\) ,已经小于要求数量,而此时其兄弟节点(按要求除非是根节点,至少有一个兄弟)的元素数量正好时临界值 \(\lceil \frac{m}{2} \rceil – 1\),此时无法通过借来满足要求,但可以用一个简单的合并操作达到要求:
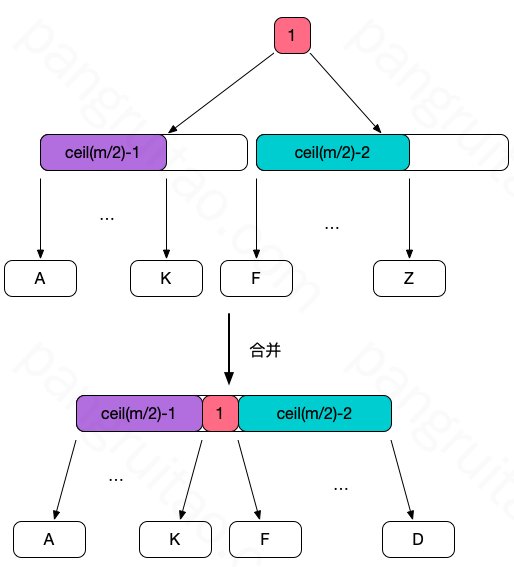
合并后,将父元素拉扯至了合并后的节点中间,计算可以发现合并后的节点元素总量为 \(2 * \lceil \frac{m}{2} \rceil – 2\),一定小于 \(m-1\) ,满足要求。同时发现其子树依旧保持顺序,意味着这个操作如同分裂一般,可以对任意位置满足条件的节点操作。
所以具体到删除问题,如果删除后关键字数量已经不足,且兄弟也在临界值,则可以将其和其兄弟节点合并:

合并过后由于父节点少了一个关键字,有可能出现两种情况:
- 父节点关键字数量不足,且非根节点,于是继续对父节点进行类删除操作(先借,借不着再合并)
- 父节点是根节点,且子树合并后空了,则删除父节点,以子树合并后的节点为根节点。