求递推数列极值的套路思考

1. 说明

递推数列极值问题在高数，或者考研数学中不时出现。通常是个难点。且主要难在其灵活性，每道题的解法看起来虽有相似之处，但有很多关键的微妙差别。

这种灵活性使看答案的时候往往惊呼妙哉，但自己面对一道全新题时却由于不能直接套经验，而不知如何下手。

我也经常卡在这种题目上。

不过思考之后，还是发现一些套路式的方式可以解决至少一半左右这样的问题。

先对递推数列有个形象化感觉。

递推数列，通常可以将条件化作，已知 \(x_0\)，且已知递推式 \(x_{n+1}=f(x_n)\)。

容易猜到，如果存在 \(\lim_{n \to +\infty}x_n=a\) ,那 a 一定满足 \(a=f(a)\)

这意味着曲线 \(y=x\) 与曲线 \(y=f(x)\) 一定有交点，且交点刚好就是极限 a。

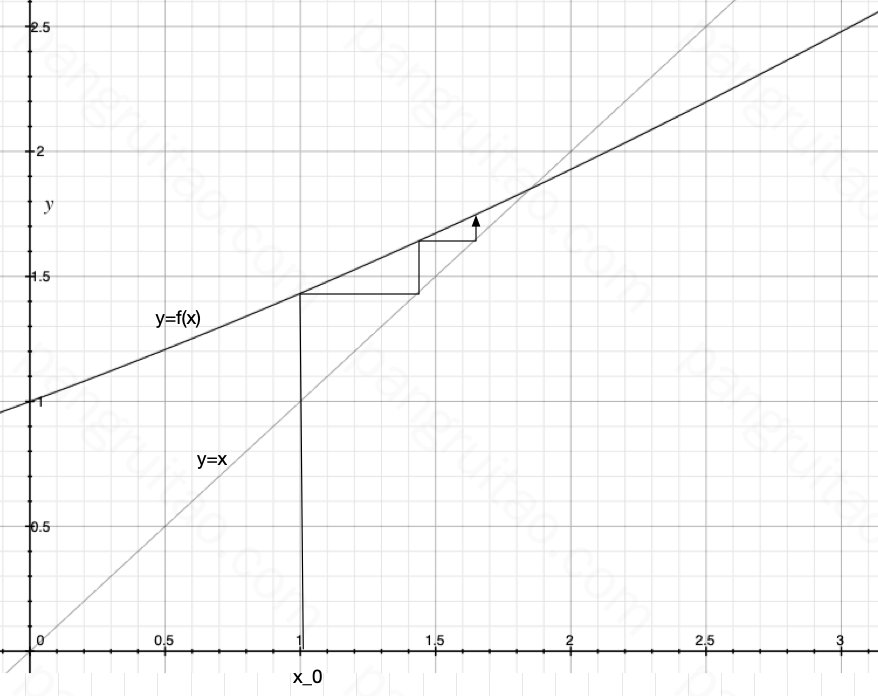
随便找了一个 \(f(x)=0.8(\ln(e^x -1)-\ln x) +1\)。

研究一下 x 到底是怎么迭代的，可以发现就是图中的那根折线，弯弯曲曲向交点收敛，且从图上来看，明显当 x 取一个大于交点的值时，也能收敛。甚至

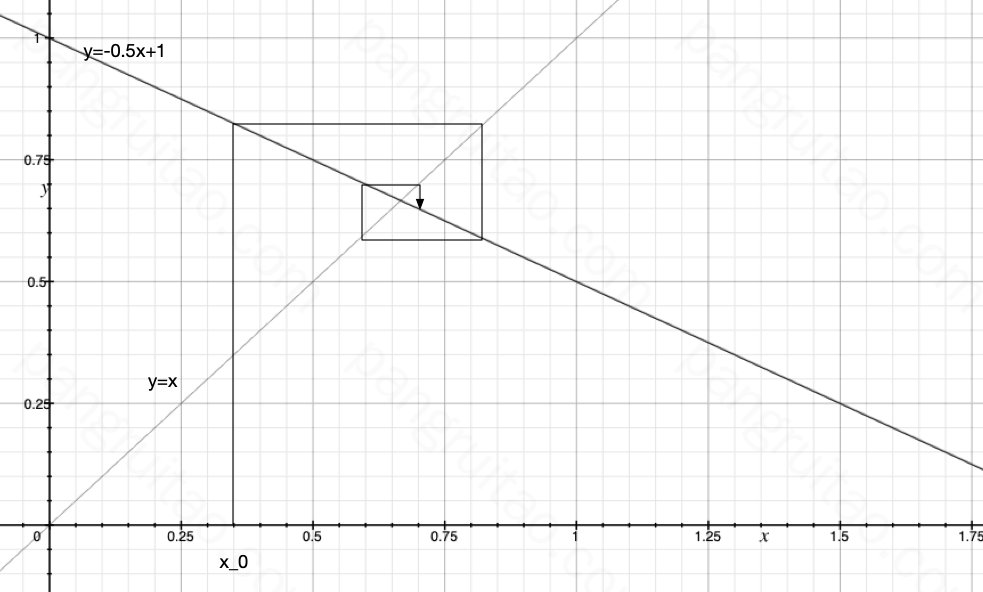
这样的 f(x) 也是可以让数列震荡收敛的。

那什么情况下数列不会收敛呢，熟悉这种图之后，会发现，当 \(|f^{‘}(x)|>=1\) 时就不再收敛了，如下图：

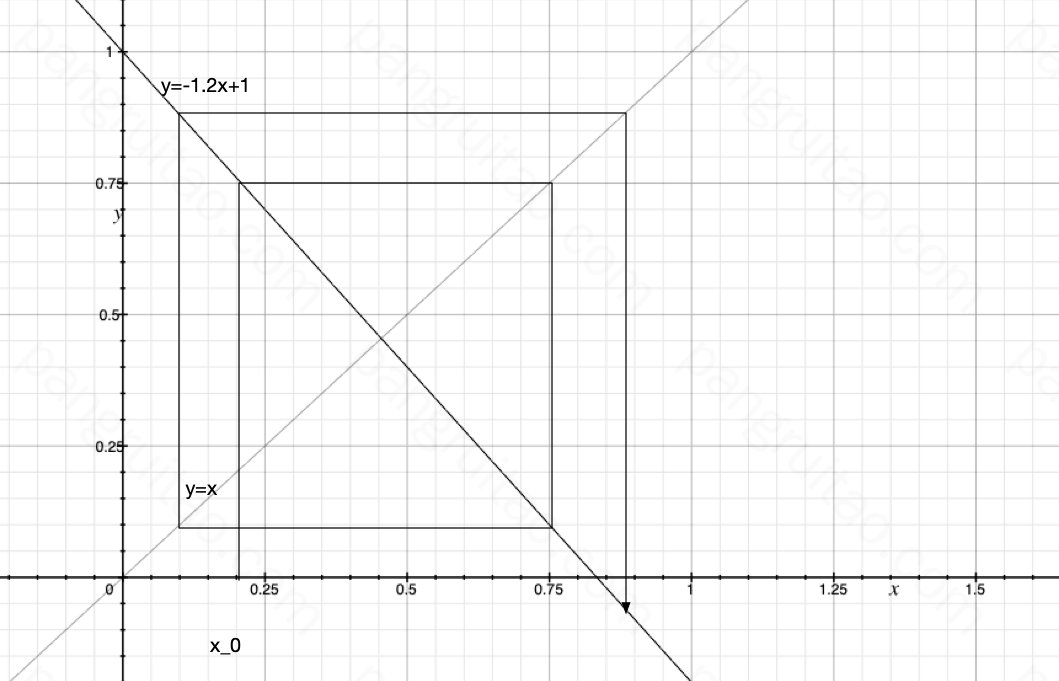
这给了两个启发：

而一旦证明极限存在剩下就对 \(x_{n+1}=f(x_n)\) 两边求极限即可得到结果。

于是接下来就是思考，怎么把这两个启发补全成证明。

根据题目条件，应有 \(x_n – x_{n-1}=f(x_{n-1})-f(x_{n-2})\)

如果 \(f(x)\) 满足 x 取值区间内，导数连续。利用拉格朗日中值定理，有 \(x_n – x_{n-1}=f^{‘}(\xi)(x_{n-1}-x_{n-2})\)

如果我们能证明在某个范围内有 \(|f^{‘}(x)| \leq a<1\)，且所有 \(x_n\) 属于这个范围。

则 \(\lim_{n \to +\infty}|\frac{x_n – x_{n-1}}{\xi)(x_{n-1}-x_{n-2}}|<1\)

则级数 \(\lim_{n \to +\infty} \sum_{i=1}^{n} (x_n – x_{n-1})\) 收敛

则 \(\lim_{n \to +\infty} (x_n – x_{1})\) 存在

即 \(\lim_{n \to +\infty}x_n\) 存在，所以可以对 \(x_{n+1}=f(x_n)\) 两边求极限的到结果。

如果 \(f(x)\) 满足 x 取值区间内，导数连续，还是利用拉格朗日定理，有 \(x_n – x_{n-1}=f^{‘}(\xi)(x_{n-1}-x_{n-2})\)

如果可以证明在某个范围内有 \(f^{‘}(x)>0\) ，且 \(x_n\) 在这个范围内

则意味着 \(x_n – x_{n-1}\) 与 \(x_{n-1}-x_{n-2}\) 同号。具体符号可以算出 \(x_1,x_2\) 后的到，以次证明了单调。

再根据 \(x_0\) 的取值，和 \(f(x)\) 的性质，找一个下界（这步还是要点灵活性，但一般不会太难），便可以凑齐单调有界

得到 \(\lim_{n \to +\infty}x_n\) 存在，也可以对 \(x_{n+1}=f(x_n)\) 两边求极限的到结果。

部分很极限的题目可能不满足这两个条件。

不过对多数递推题目而言，应该是可用的。