1.前序遍历
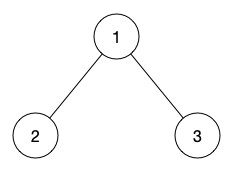
定义
- 对任意子树,优先访问根节点,再左子树,再右子树。
遍历
- 遍历时需使用栈保存根节点,用以未来访问右子树使用。
特征
- 第一个为整棵树的根
- 最后访问一定为叶节点。
2.中序遍历
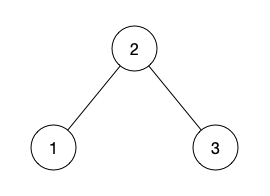
定义:对任意子树,优先访问左子树,再访问根节点,再访问右子树。
遍历:遍历时需要使用栈保存根节点,用以未来访问根节点和右子树使用。
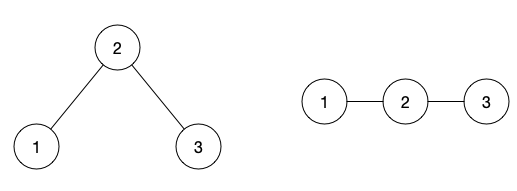
特征
- 中序遍历结果正好是将整棵树“压扁”之后得到的序列,所以也可以依据中序序列容易地对树进行切割划分。
- 第一为最左的节点
- 最后为最右的节点
3.后序遍历
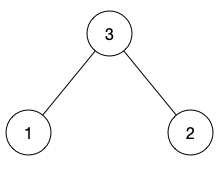
定义
- 对任意子树,优先访问左子树,再访问右子树,最后访问根节点。
遍历
- 需要使用栈保存根节点,用于后续访问其右子树和根节点。
特征
- 最后一个为根
- 第一个为最偏左的叶子节点
4.确定二叉树
中序与任意前序或后续可以唯一确定一棵二叉树。方式为根据前序或后续确定根,并在中序中根据根将树二分为左右子树。
如对于前序abcdefgh,和中序cbdagfhe:
首先以前序第一元素a为根,在中序中切分
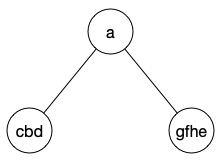
分别在前序中找cbd和gfhe中的第一个元素,为b和e,于是在中序中进行进一步切分
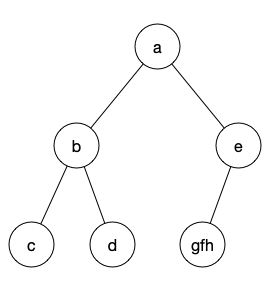
最后再对gfh子树施以相同的操作,得到
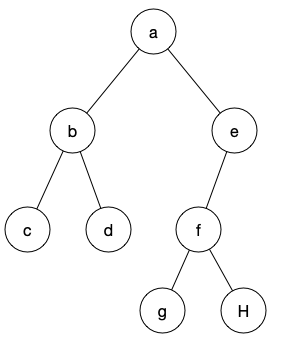
5.前序与后序组合
前序与后续组合也无法确定二叉树形态。但我们依旧可以通过前序和后序获取一些信息:
- 非祖系关系的元素在序列中的相对位置不变,所以如果前序和后序有相对位置不变的元素或元素集,则一定非直系关系。
- 如果两元素在前序中为…X…Y…,在后序中为…Y…X…。则X是Y的祖先。
6.前序对中序的限制
在已知前序的情况下,合法的中序会有什么样的性质呢?
前序序列和中序的关系限制相当于以前序序列为入栈顺序,以中序序列为出栈顺序。其组合数量可参考卡特兰数。
如前序为:abcdefgh,考虑其中序的可能性
首先Push(a),之后可以选择立刻Pop(),也可以选择稍后Pop()。
- 当Pop出任意元素,比如a,则从此开始构建a的右子树
- 如果不Pop,则从当前位置继续向左子树构建
其原理可以参考前方的“4.确定二叉树”。
于是可以用栈的思路对中序进行限制:当前序中某几个元素位于栈内时(已经Pop之后的某元素,但没Pop它们),则它们的出栈顺序(中序中的顺序)一定和入栈顺序(前序中的顺序)相反。
后序对中序的限制也是相同的道理,仅需修改为从后往前入栈。