2.0 零散点
重点
- 奇偶校验:凑成奇数个1或者偶数个1
- 变形补码:模4补码
- 规格化后需使尾数绝对值>=1。对于负数补码则应为 11.XXXXX.. 负原码则为 11.XXXX(不带符号位)
- 串行进位、并行进位(单级先行进位、多级先行进位)
- 用移码表示浮点数阶码的好处:
- 相比于原码和补码,移码比较大小更方便
- 检验特殊值比较容易
2.1 数制与编码
进位计数法
- 对于任意 r 进制数 (\(K_n K_{n-1} K_{n-2}…K_{0} K_{-1}…K_{-m}\)),其值等于
begin{align}
sum_{i=-m}^{n} K_i*r^i
end{align}
- 各种进制转换方式
- 十转二,二转十
- 二转八转十六,十六转八转二
- 十转八,八转十
- 通用方式
- 整数部分除基取余
- 余数部分乘基取整
各种码
- BCD码
- 8421码
- 余3码:8421基础上加 \((0011)_2\)
- 2421码
- ASCII码
- 仅0~126
- 汉字的表示和编码
- 输入编码
- 汉字内码
- 汉字字形码
- 区位码:排列于 \((94)_{10}*(94)_{10}\) 矩阵,4位10进制数
- 国标码:区位码转16进制后 + 2020H
- 汉字内码:国标码 + 8080H
- 校验码
2.2 定点数的表示和运算
小数点位置
- 最高位之前:定点小数
- 最低位之后:定点整数
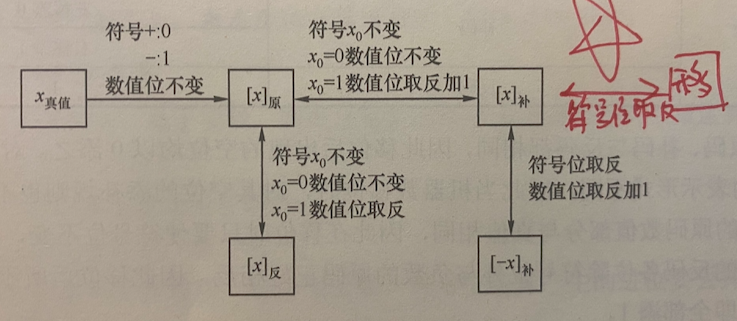
原码
- 首位表示符号,1为负
补码
- 首位如果为整数部分第r位(包括第一位),则其权值为 \(-2^{r-1}\)
- 算术移位
- 将符号位和数值位一起右移并保持符号位不变等效于除以2
- 非首位部分显然被除以2.首位由0变为00,或由1变为11,按定义,对应的值也刚好是除以2
- 如果首位和次首位都为1,可以用相反操作进行乘2
- 将符号位和数值位一起右移并保持符号位不变等效于除以2
- 模4补码
- 取反操作:符号位取反,数值位取反加1
反码
- 负数时,表示为其相反数的按位取反
- 任意x加自身的反码得到全1码
移码
- 基于真值加一个偏置值 通常加 \(2^n\) 其中n为机器字长减一
- 0表示唯一
- 移码和补码的首位刚好相反
- 移码全0时最小,对应真值 \(-2^n\)
转换关系
运算
- 算术移位
- 乘2或者除2
- 原码保持符号位
- 补码右移补符号位
- 逻辑移位
- 视为无符号数移动
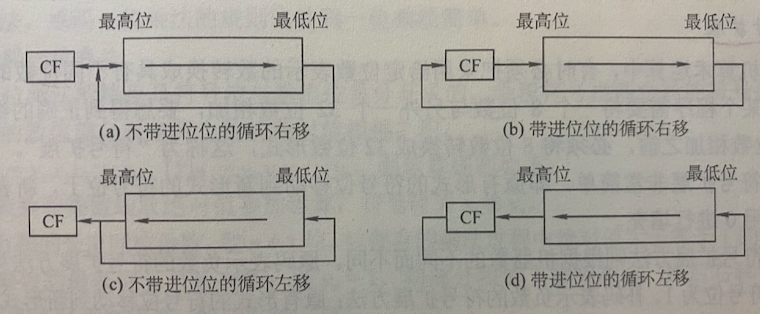
- 循环移位
- 可带上进位 CF 移位
- 原码加减
- 先判断符号位,相同则直接加,不相同则绝对值大的减绝对值小的
- 补码加减
- 直接加减,并丢弃溢出位
- 符号扩展
- 溢出判断
- 乘法运算
- 原码
- 补码
- 除法运算
- 原码
- 补码
数据存储
- 大端方式
- 起始地址放高位
- 小端方式
- 起始地址放地位
- 边界对其
2.3 浮点数的表示与运算
表示
- 格式
- 阶符+阶码数值+数符+数值
- 规格化
- 左规、右规
- IEEE 754标准
- 数符+移码表示的阶码+原码表示的数值部分
- 其中移码的偏置值为 \(2^{n-1} – 1\)
| 类型 | 数符 | 阶码 | 尾数数值 | 总位数 | 偏置 | 偏置 |
| float | 1 | 8 | 23 | 32 | 7FH | 127 |
| double | 1 | 11 | 52 | 64 | 3FFH | 1023 |
| temp | 1 | 15 | 64 | 80 | 3FFFH | 16383 |
和定点相比较
- 范围更广、有效位数低、运算复杂、溢出判断同时需要考虑阶和数
加减运算
- 过程
- 对阶
- 尾数求和
- 规格化
- 舍入
- 溢出判断
2.4 算数逻辑单元(ALU)
加法器
- 串行
- 并行
- 分组并行进行
- 组内并行,组间串行(单级先行进位)
- 组内并行,组间并行(多级先行进位)
- 分组并行进行
- 每一位求和 与 进位的逻辑表达式
ALU功能和结构
- 组合逻辑电路,能进行多种运算